Convergence studies for computational homogenisation

Table of Contents

• Geometry, material properties and finite element meshes
• Results

This document describes the importance of high-order geometry approximation for the multi-scale computational homogenisation. Both h- and p- convergence studies are performed while considering 1st and 2nd order geometry approximations. The p-convergence here based on hierarchic finite element method.

How to cite us?

Geometry, material properties and finite element meshes

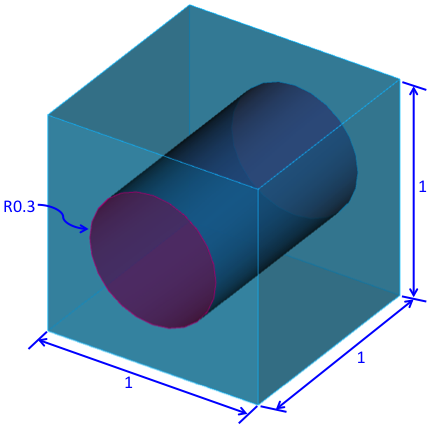
The representative volume element (RVE) considered in this case is a cube of unit dimensions consisting of a single yarn and matrix and is shown in the following figure. The yarn is of circular cross-section with radius of 0.3 mm.

RVE geometry (all dimensions in mm)

Isotropic and transversely isotropic material models are used for the matrix and yarns respectively, the material properties for which are given as:

Matrix:

• Young’s modulus = 3.5 GPa
• Poisson's ratio = 0.3

Fibres:

• Young’s modulus in transverse direction E_p = 35 GPa
• Poisson's ratio in transverse direction v_p = 0.26
• Young’s modulus in fibre direction E_z = 70 GPa
• Poisson's ratio in fibre direction v_pz = 0.26
• Shear modulus in the fibre direction G_pz = 17.5 GPa

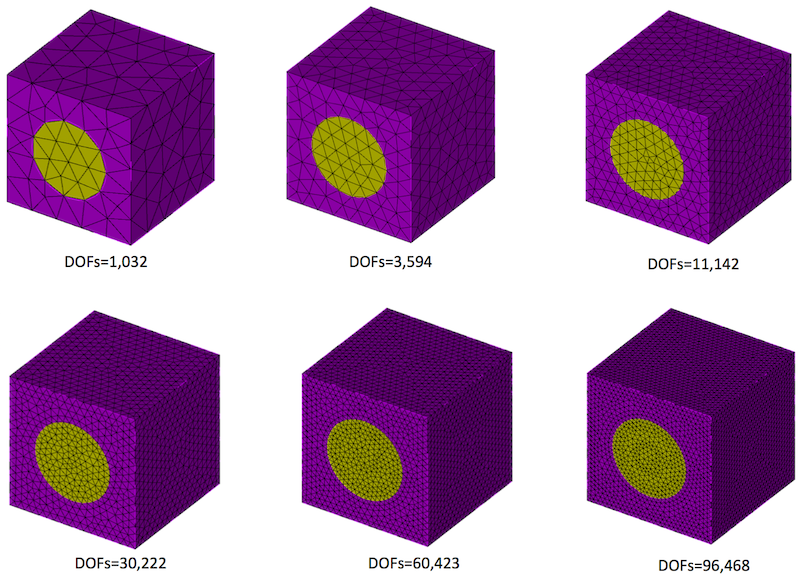
The following six FE meshes are considered for the h-convergence studies for both 1st and 2nd order geometry approximation, where degrees of freedom are increasing for the 1st to last. Each of these FE meshes is not refinement of the previous FE mesh but the geometry is remeshed from scratch using automatic meshing in CUBIT. In each of the consecutive finer mesh geometry is represented accurately relative to the previous case. The degrees of freedom in the consecutive discretisation are 1032, 3594, 11142, 30222, 60423, 96468 respectively. In case of p-convergence studies the 1st mesh with 1032 DOFs is considered for both 1st and 2nd order geometry approximations.

RVE meshes used in the convergence studies

The commands used for this example is given as follows, the output of which is full homogenised stiffness matrix for linear displacement, uniform traction and periodic boundary conditions cases.

mpirun -np 1 ./rve_fibre_directions -my_file cube_with_reinf_06.cub -ksp_type fgmres -pc_type lu -pc_factor_mat_solver_package superlu_dist -ksp_monitor -my_order 1

mpirun -np 1 ./rve_mechanical -my_file solution_RVE.h5m -ksp_type fgmres -pc_type lu -pc_factor_mat_solver_package mumps -ksp_monitor -my_order 1 -my_bc_type disp

Results

The above-mentioned RVE is solved using the periodic boundary conditions. The h- and p-convergence for both 1st and 2nd order geometry approximation for the homogenised coefficients of the stiffness matrix, i.e. C11, C22, C33, C44, C55 and C66 are given in the following figure. Higher value of these coefficients for the 1st mesh in the case of 2nd order geometry approximation is due to the greater yarn volume. It is clear from these convergence plots that for a relatively coarse mesh and using 1st order geometry approximation, p-convergence can leads to wrong homogenised stiffness matrix. For the 1st order geometry approximation C33 is increasing with h-refinement while decreasing with p-refinement. In the case of 2nd order geometry approximation both h and p refinements leads to similar results.

Convergence of homogenised C11, C22, C33, C44, C55 and C66