 |
v0.14.0 |
 |
v0.14.0 |
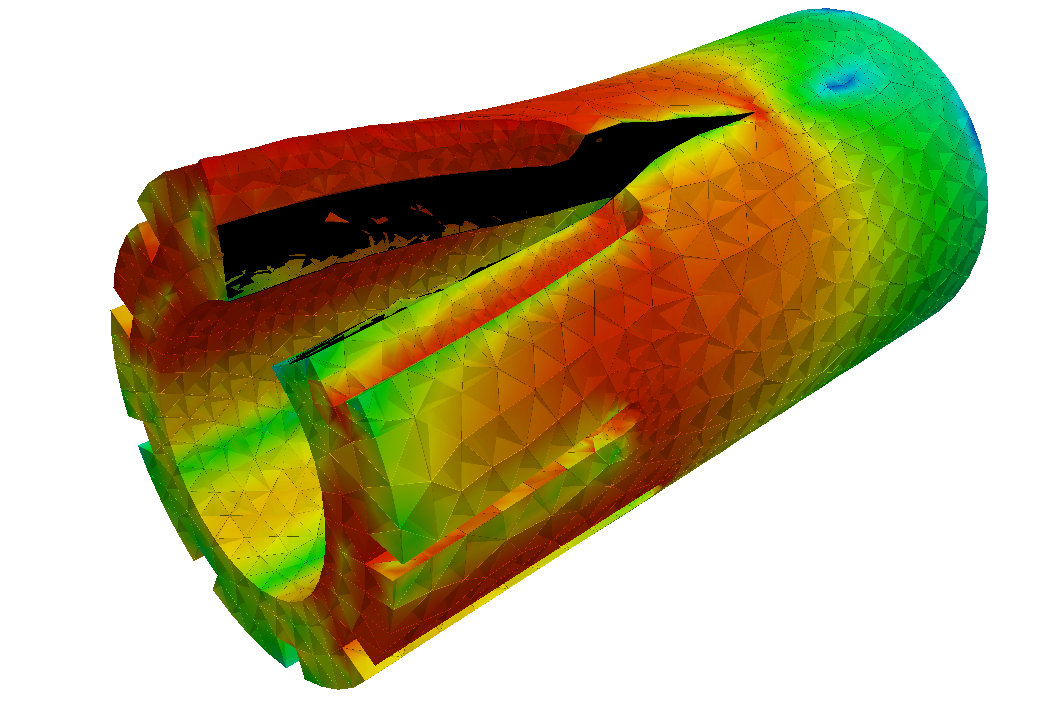
The following tests have been designed to check the capability and robustness of crack propagation tools in MoFEM.
Three test are investigated,
Full test specification and geometrical description is available here: link.
This work is motivated by the inability of commercial finite element codes to simulate crack propagation in brittle materials in structural elements with complex geometries.
All calculations presented in this document are based on the theoretical developments presented in paper by Kaczmarczyk & Pearce [38], whereby the equations for equilibrium and propagation of the crack front are derived from first principles, i.e. the first law of thermodynamics and principle of maximum dissipation of energy (particular case of second low of thermodynamics). The methodology is formulated in the context of configurational (Eshelby) mechanics. Conservation of momentum is solved in both the spatial and material domains. The spatial (or physical) domain can be considered as a description of what we physically observe and the material domain is the evolving reference domain due to crack evolution. The crack front is subjected to a constraint emerging from the Griffith fracture criterion.
In addition to the theoretical developments, to realise the propagating crack with finite elements, a method based on face splitting is proposed in [38]. However, in the current work, an alternative and novel approach is proposed, leading to an implicit, smooth and consistent crack propagation. In the following tests, cracks are propagated by directly displacing crack front nodes in the material reference configuration. This approach is distinct to well known methods, where the crack propagation is realized by enriching nodes (X-FEM), re-meshing or face splitting. This method enables the crack front to move continuously by an arbitrary, implicitly calculated, distance, based on crack front equilibrium condition subjected to Griffith criterion; in classical approaches, the crack is extended by some discrete predefined distances.
In the presented approach, smooth evolution of the crack geometry results in a certain amount of mesh distortion. To resolve this, an efficient mesh smoothing technique is implemented in VolumeLengthQuality (see [38]) and surface constraints are implemented in SurfaceSlidingConstrains. This result in a variant of the Total Arbitrary Lagrangian Eulerian Formulation (T-ALE), such that mesh smoothing does not influence the crack propagation.
In addition to mesh smoothing, a face flipping, node merger and edge splitting algorithm is incorporated to fully propagate the crack over the entire thickness of the body. After each converged load step, topological mesh changes are introduced to improve mesh quality in the neighborhood of the crack front. It should be noted that at this point, the crack geometry is fixed and not influenced by mesh changes. In other words, re-meshing and/or face flipping is not used here to realise the crack propagation but to maintain mesh quality. Poor mesh quality is a major source of error.
A finite element in T-ALE setting is implemented in NonLinear Elastic Element. Spatial and material forces are calculated, which drives body deformation in the physical space and crack front displacements in the material space. Material forces acting on the crack front are equilibrated by Griffith forces (material resistance forces). Griffith force element is implemented in GriffithForceElement.
In this approach crack propagates only in mode-I. The crack front position and direction are calculated implicitly at the same time, in such a way that maintains equilibrium at the crack front at the end of load step. In classical approaches, equilibrium is condition is not used, only the Griffith (or other) criterion is applied, and crack is extended based on the stress state at the beginning of the load step. Since crack evolution is strongly nonlinear, this classical approach can result in a mixed mode crack extension, demanding an appropriate calculation of crack direction for mixed mode, leading to an explicit calculation of the crack path. It is important to stress that propagating cracks in mode-II or mode-III are usually not observed experimentally in homogeneous isotropic solids. A crack subjected to mode-II or mixed mode loading, curves or kinks and propagates in a direction that maintains locally pure mode-I conditions at the tip [22] [34]. This is consistent with the approach we have adopted, achieving maximum dissipation of energy in the generation of new crack area and crack front equilibrium.
In all tests, it is assumed that the crack is propagating quasi-statically. This assumption is satisfied by controlling the force such that material displacements of the crack front lead to slow total crack area increase. To achieve this, a specific version of the arc-length technique is adopted, see [38] for details. Since crack propagation is understood here as an evolution of the body topology and a strongly non-linear process, each increment of the crack area is controlled during the incremental iterative process, and the crack area size is automatically adapted to obtain the desired number of Newton-Raphson iterations for each load step.
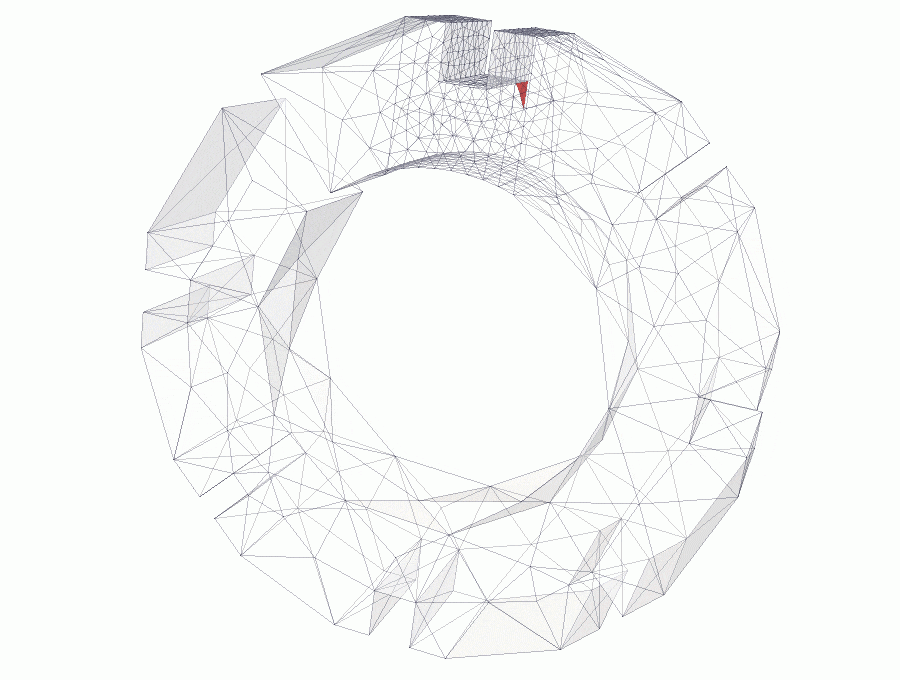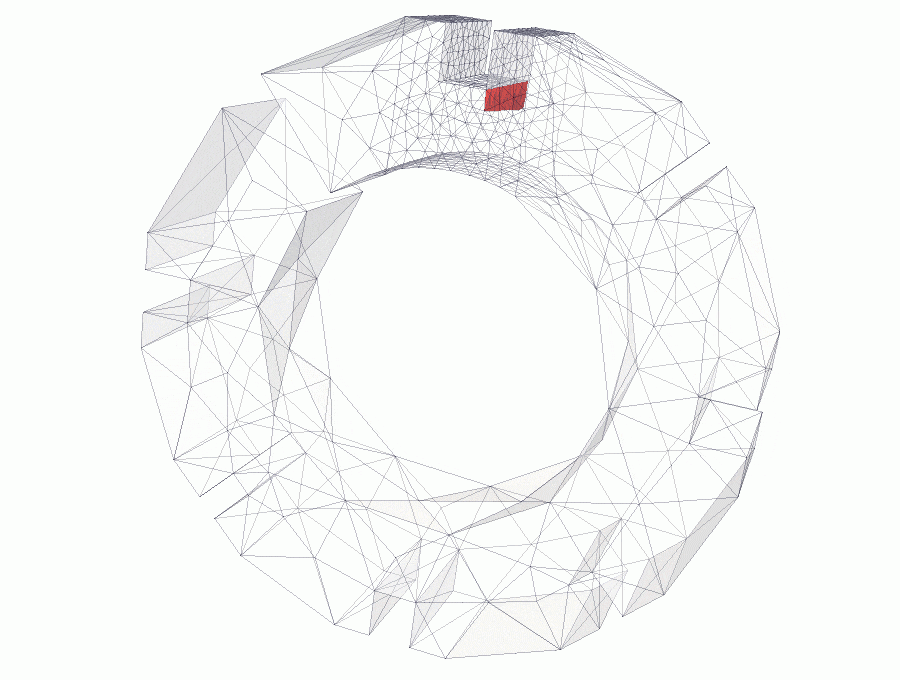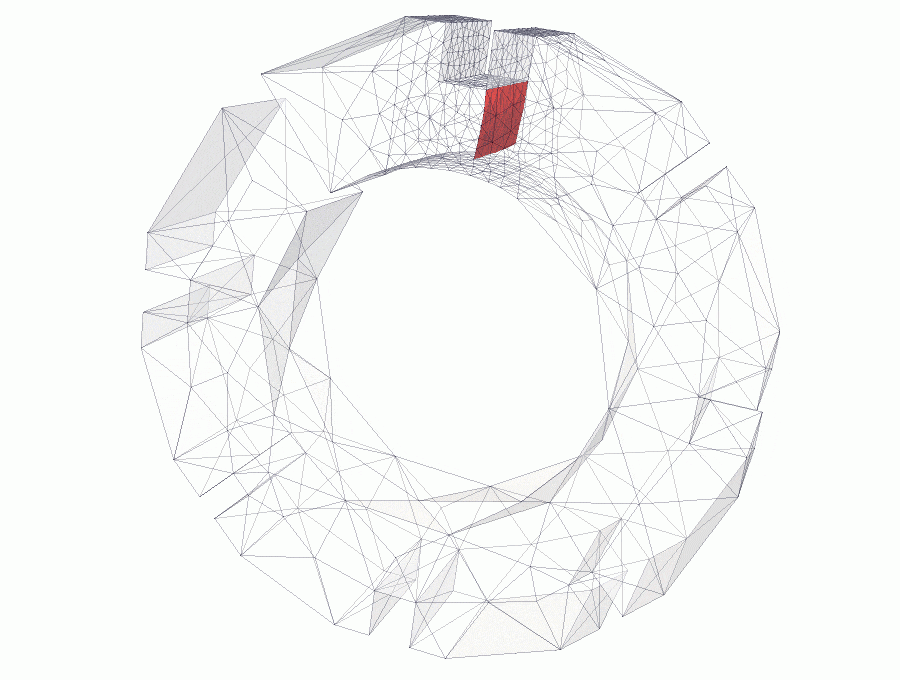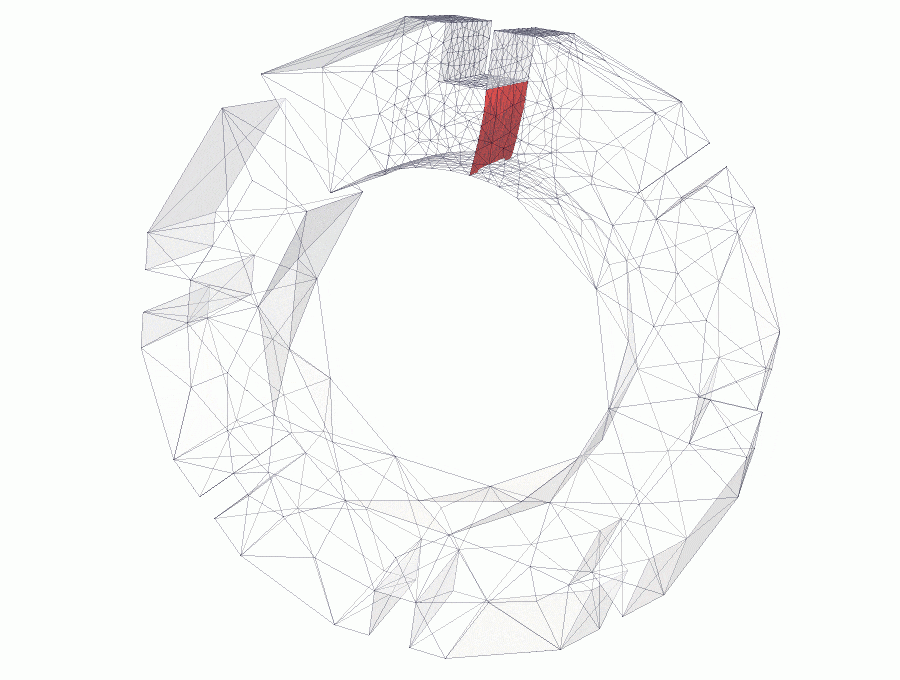
A brick slice is subjected to forces applied on top and bottom slot edges. Edge forces have the same magnitude but opposite directions, that produce a couple and pure bending moment is applied, see link for details.
Crack is initialised at the keyway corner. The size of the initial notch is defined by the mesh size. Initial analyses show that size or shape of initial notch does not influence significantly the final crack propagation.
Since the slice is subjected to pure bending, at any arbitrary cross section of the brick, no net axial force is present. As a result, material points in the vicinity of the crack front are subjected to tension; near the bore, material is in compression. Therefore, the crack is prevented from propagated fully through the brick and an elastic hinge is created at the end of the analysis.
It can be noted that any partial crack propagation through the bore would lead to self penetration of the crack surfaces, since compressive stresses are acting next to the bore, to transfer the externally applied bending moment. It is postulated that inability of the presented method to propagate the crack through to the bore validates the crack front equilibrium equations derived in [38]. The crack can only propagate if the crack tip is subjected to tension. Given that only pure bending is applied, the crack front can only move as far as the neutral axis (in extreme). The neutral axis is half the distance between crack front and bore surface, where tension and compression is applied, respectively. Therefore, in each load step, in the limit, a crack can propagate half of its previous distance, and so on for the following steps. As a result, the crack will only reach the bore in an infinite number of steps (this justification is valid for ideal structure, assuming of small strains and displacements).
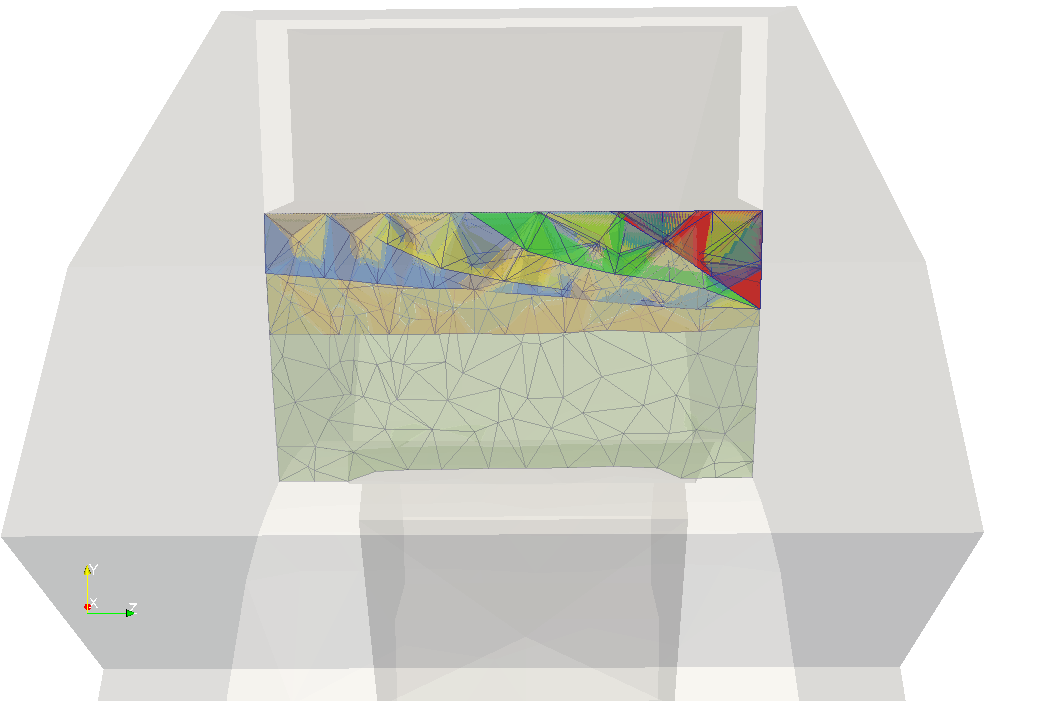
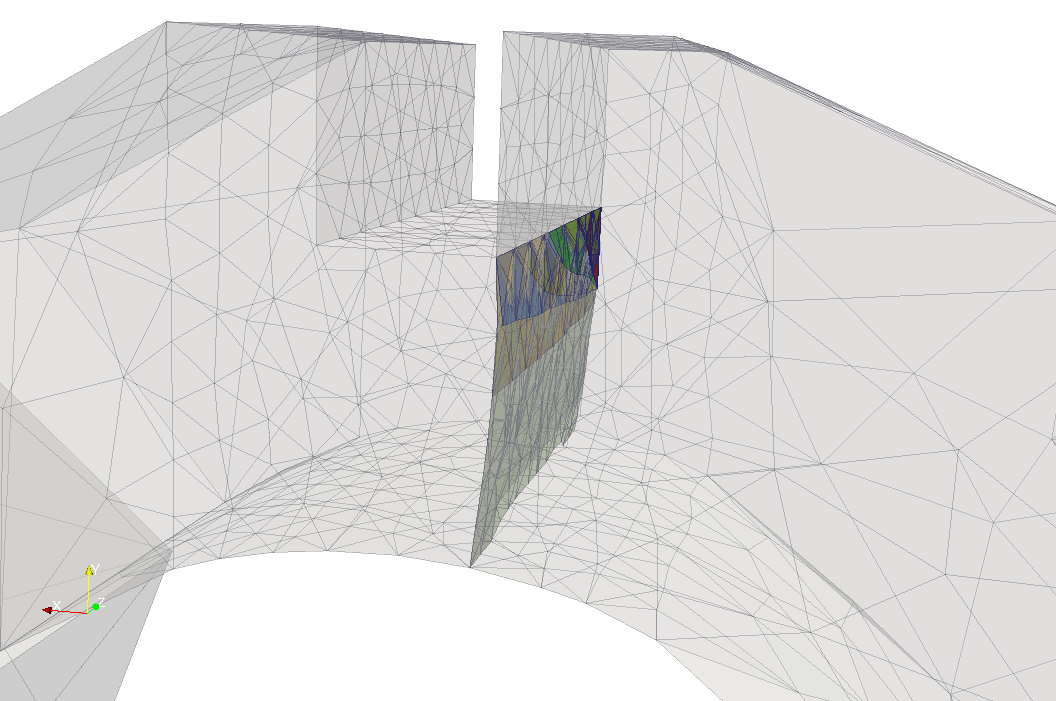
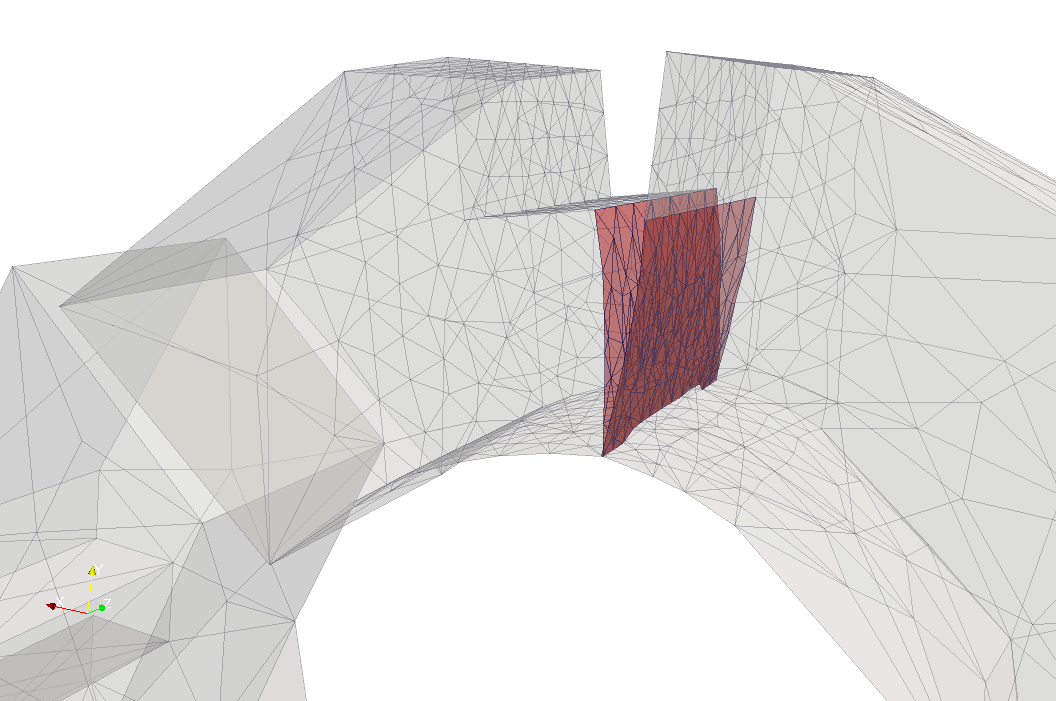
The figures above show snapshots of crack propagation, where the red triangle represent initial crack notch. Note that crack propagation is not planar and bends slightly towards the slot.
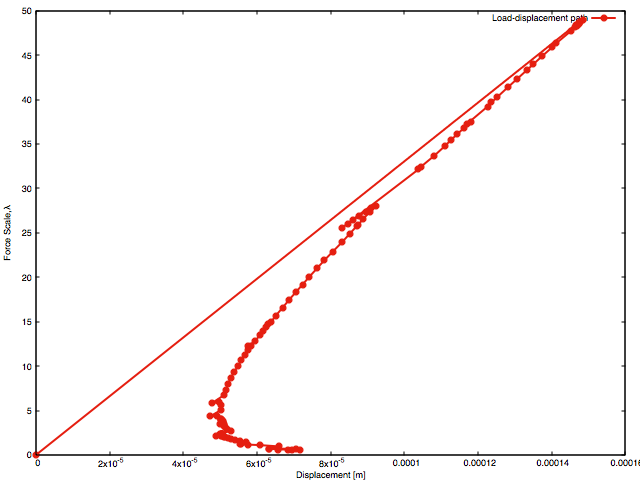
The figure above shows the load-displacement path, with generalised displacement on the x-axis and force load factor, on the y-axis. The generalised displacement does not represent a particular point on the structure, but its value is work conjugate to the applied forces and is calculated from the following formula,
\[ \Psi = \frac{1}{2} u (\lambda f),\; \textrm{thus}\quad u = 2 \frac{\Psi}{\lambda f} \]
where \(f=1\)[N] is reference force, \(\Psi\) is elastic energy, \(\lambda\) is load factor and \(u\) is generalised displacement. The generalised displacement is used to present results objectively. The load-displacement plot is obtained using arc-length control, such that the external force is adapted to maintain the crack area during each load each step. This results in a unique maximum dissipative load path. Since maximum dissipation of energy drives crack propagation direction, this plot represents the equilibrium path. The crack surface is the result of maximum release of energy, therfore any other shape of the crack front or crack surface would release less strain energy. However, for further verification those calculations should be repeated for denser meshes and higher order of approximation order, to verify the quality of the finite element approximation itself.
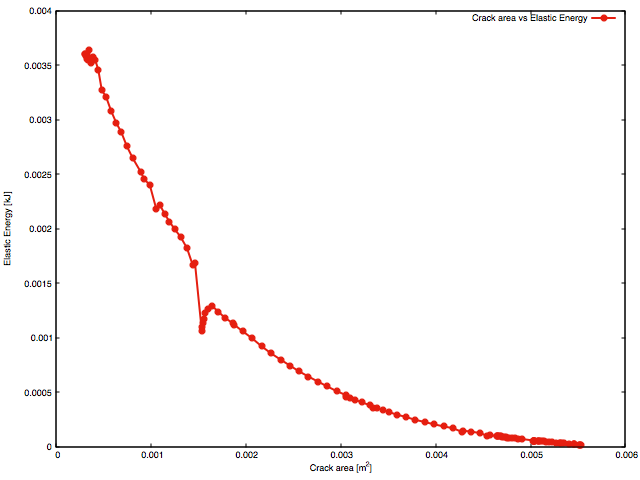
It should be noted that the energy release rate is assumed constant ( \(g_c\)) and a material parameter. However on the structural level, the crack area vs strain energy plot shows that the slope of curve is not constant over the analysis. The explanation for varying slope of curve is explained by two factors;
Note, that it can be easily shown (both analytically and numerically), that for a long (infinite) plate with a notch, the slope on the crack area vs strain energy plot is constant, since crack front length is constant and forces are applied remotely from the fracture process.
One can also note a jump in the response on both of the plots above. This is the outcome of a numerical artifact. In the current algorithm, by default, once a crack front approaches a corner, the crack is automatically extended to pass the corner. Increasing mesh density will reduce this effect. In practice, this algorithm feature can be switched off to avoid this behaviour. Cracking of the corner does not signifciantly influence the results.
The following program calculates the Griffith forces for initial crack configuration, allowing user to define refinement level at the crack front. It generates a starting file out_spatial_2_0.h5m for the crack propagation program.
where:
This program does the crack propagation,
where additional parameters are,
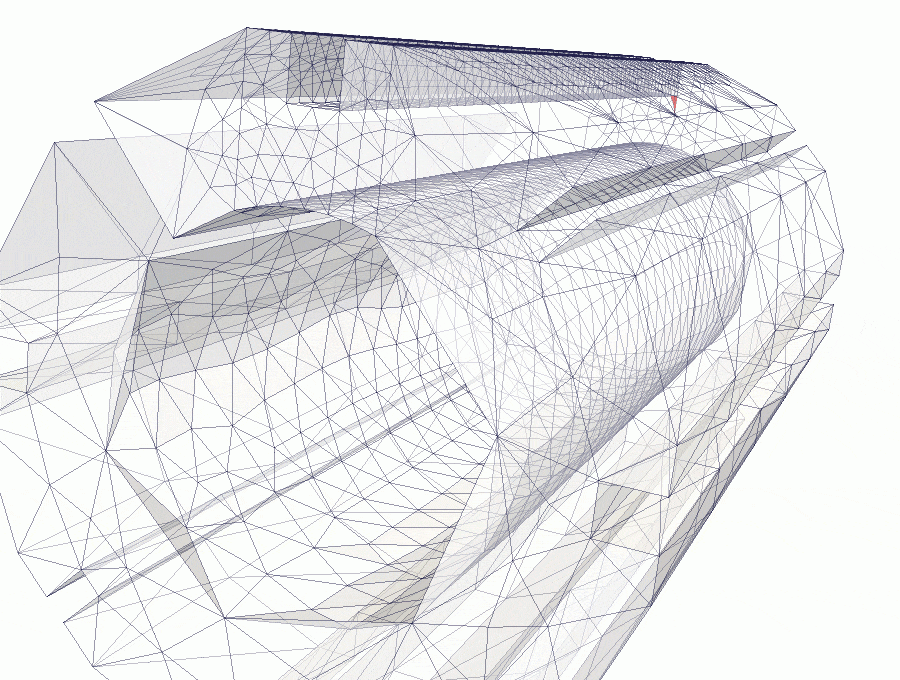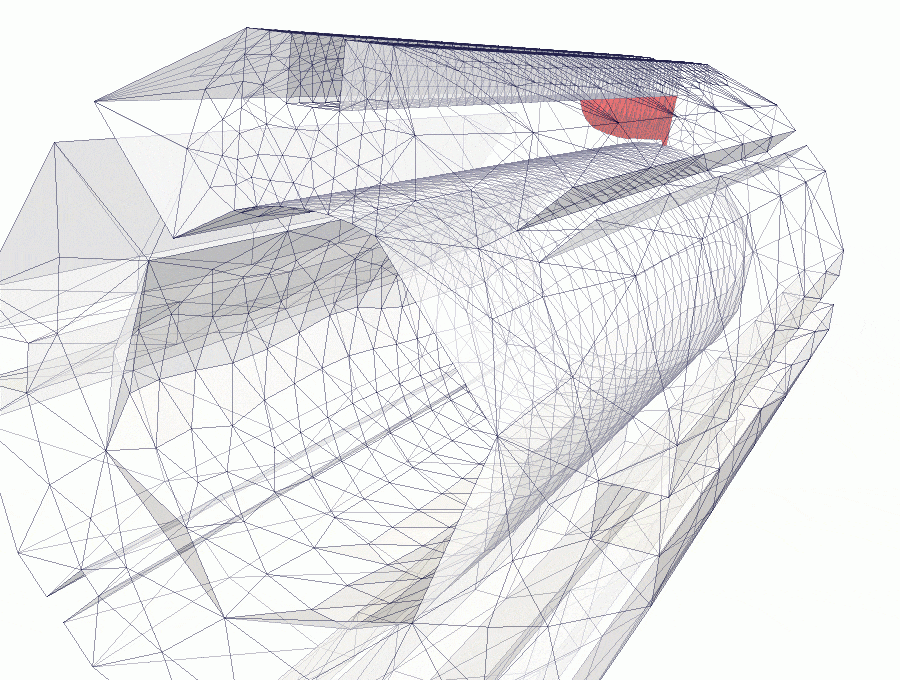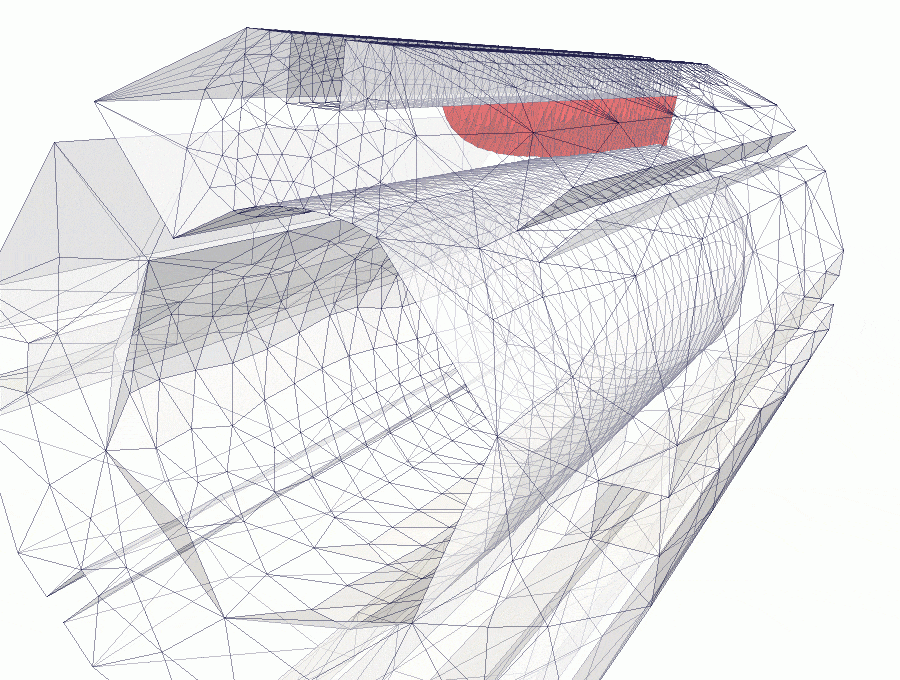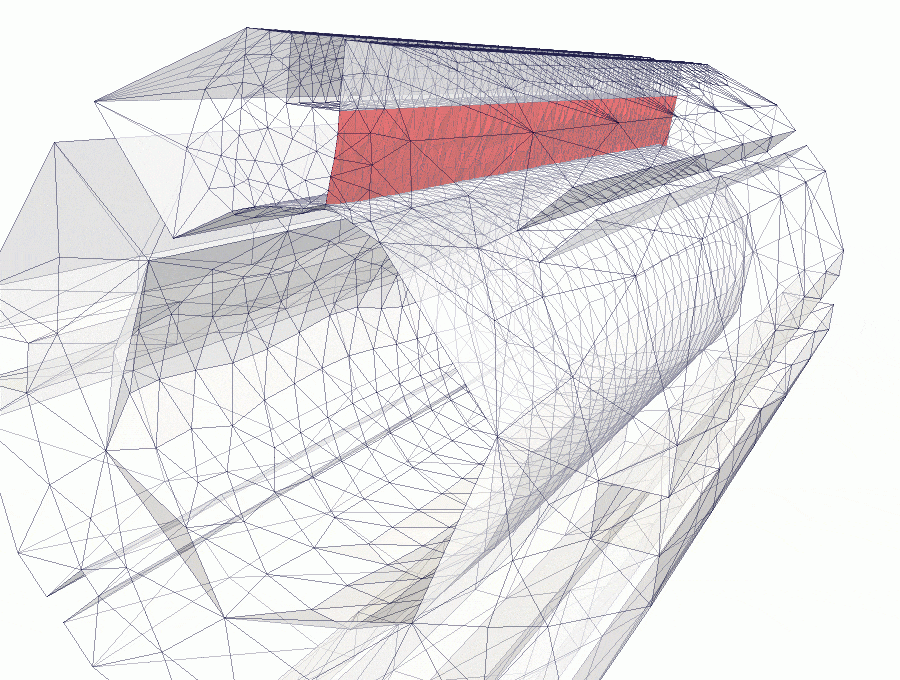

The crack propagation for full brick is similar to previous example. Crack is initiated form corner triangular notch on one of the brick sides, propagates to opposite side and then towards the bore. Since pure bending moment is applied and no axial force is present, elastic hinge is created and brick is not exhibiting a full break.



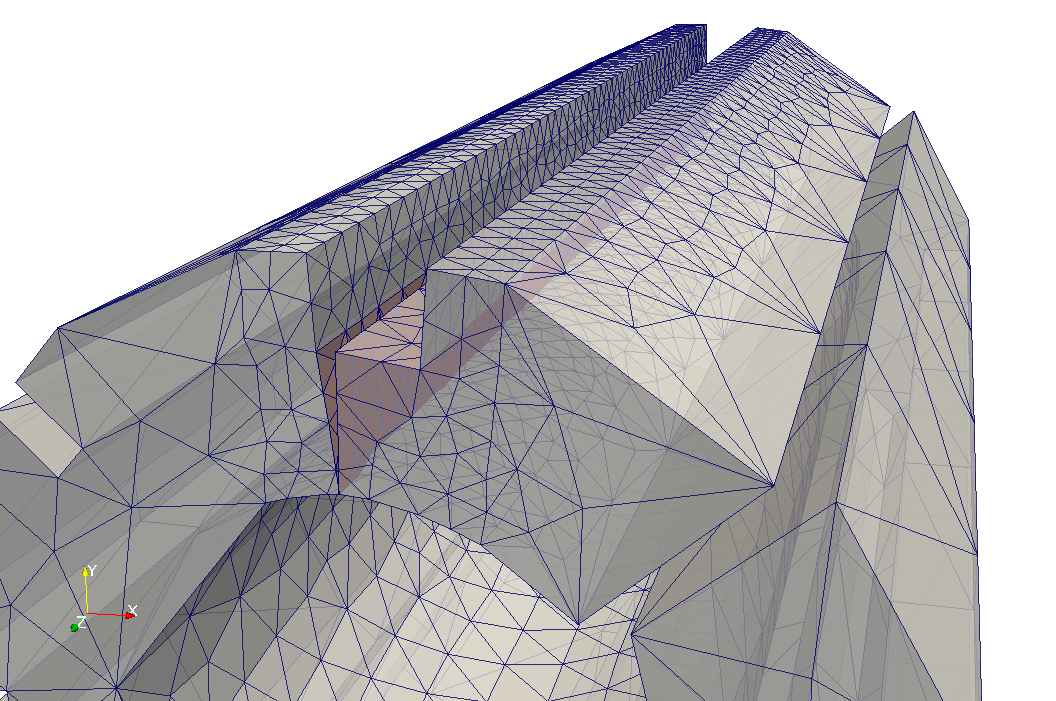
In the figures above, it is shown how crack propagates in subsequent snapshots. The crack is predominately planar during the analysis, however it approaches the surface of the bore at an angle - this can be observed in the figure presenting the brick deformation.
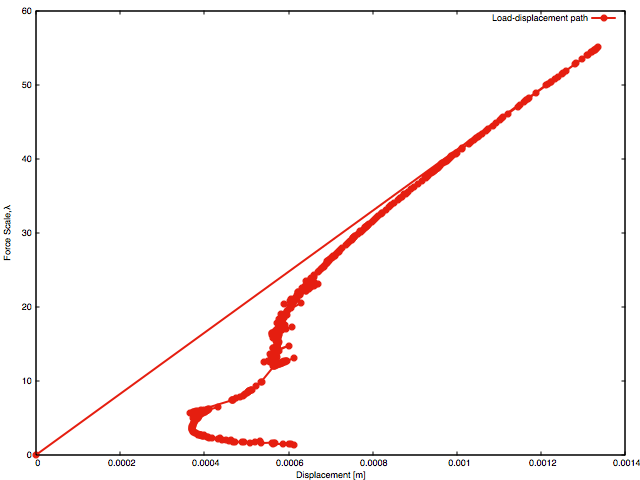
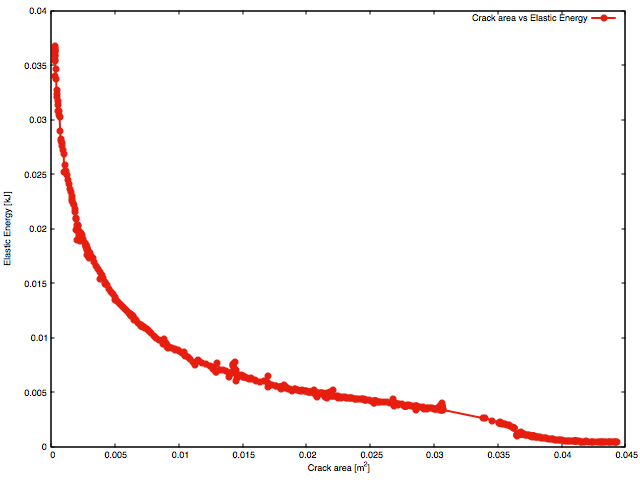
In the above, plots of load-displacement response and strain energy against crack area are shown. These are more complex than for the brick slice. Three stages of crack propagation can be identified; propagation of the crack to the opposite brick surface, propagation to the bore and finally creation of elastic hinge (where the equilibrium path achieves a quasi plateau).
Analysis of load path enables better understanding of component safety, noting that if
where \(\delta u_i\) and \(\delta \lambda_i\) are increments of displacements and forces at load step \(i\).
It can be noted that for brick slice and full brick, crack propagation is unstable, until snap-back point at the end of analysis where elastic hinge is created.
The full brick model is very similar to brick slice. The only difference is brick length which is set according to the specification in link. Code was run with the same input parameters as in previous example, only difference is that number of processors was increased to 24 and calculations were executed on ARCHIE-WEST.
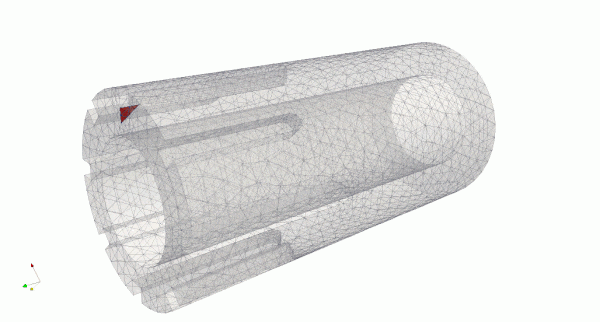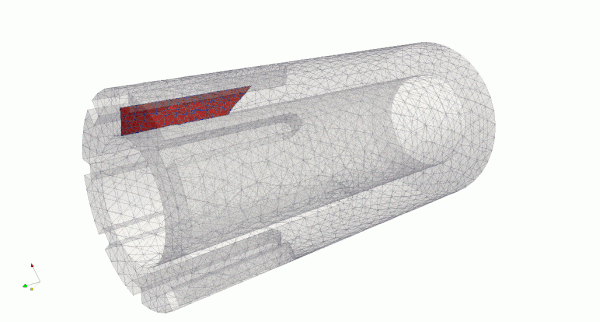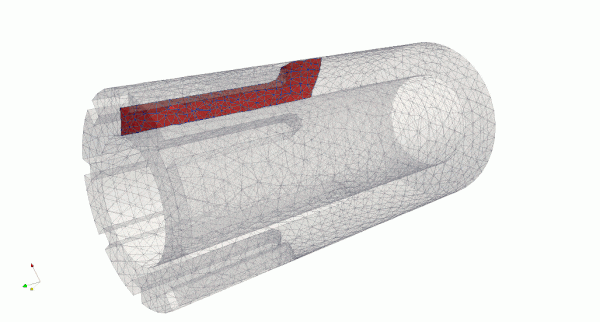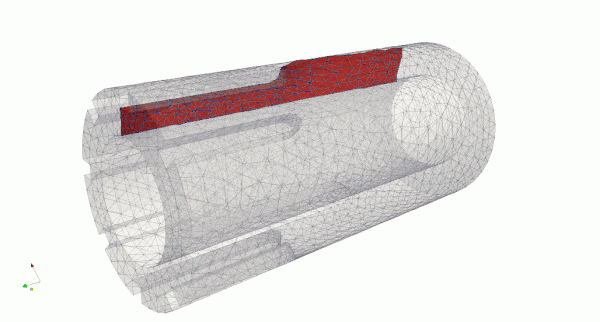
This test has complex geometry and crack propagation path compared to test 1 and test 2. See details about loading and geometry here link. A tearing load is applied at key way edges, mimicking loading from interstitial key. In this example, the crack initially propagates along the edge and then to the bore. Next it propagates along the brick to its opposite side across the brick cross section.


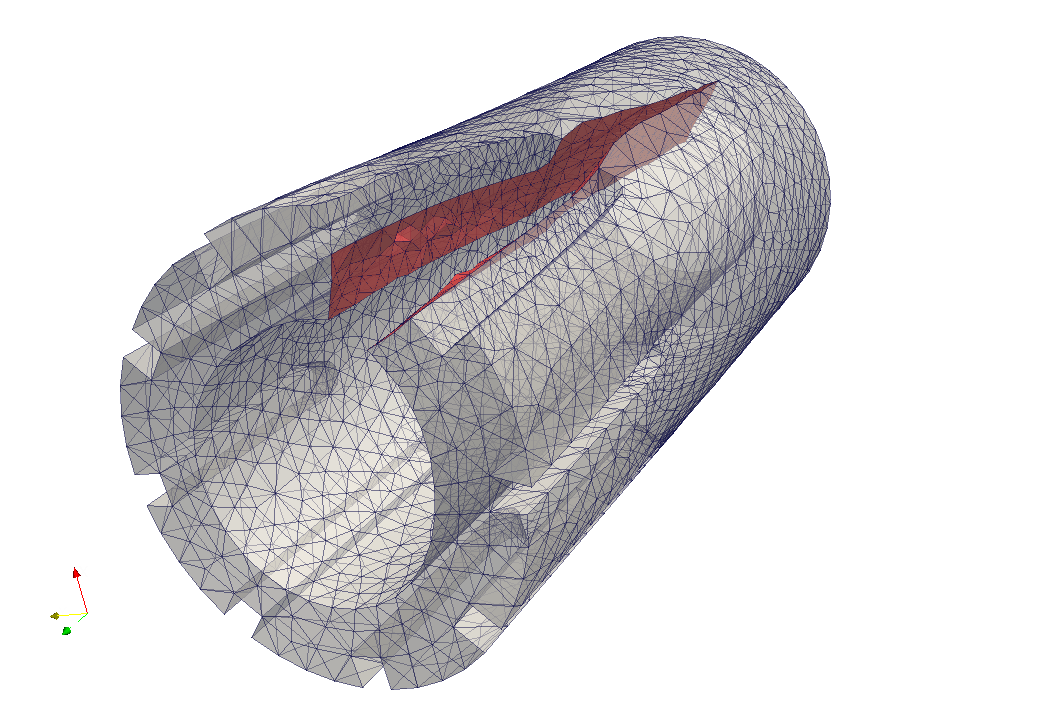
In the figures above, it can be seen that crack propagation has several stages, and initially is slightly curved and it approaches the bore at an angle. Once the crack front passes the end of the keyway, there is a distinctive curve for some distance.
In the simulation of this test, the code encountered some difficulties due to the relatively coarse mesh. Calculations have been stopped just before crack front reach opposite side due to deterioration of mesh quality. This difficulty will be removed in next MoFEM release.
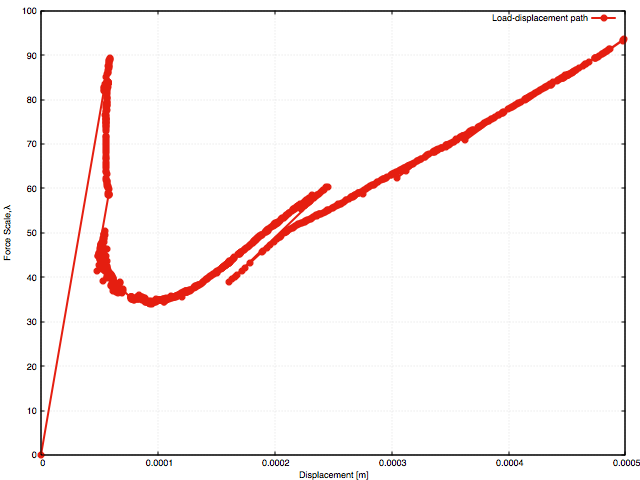
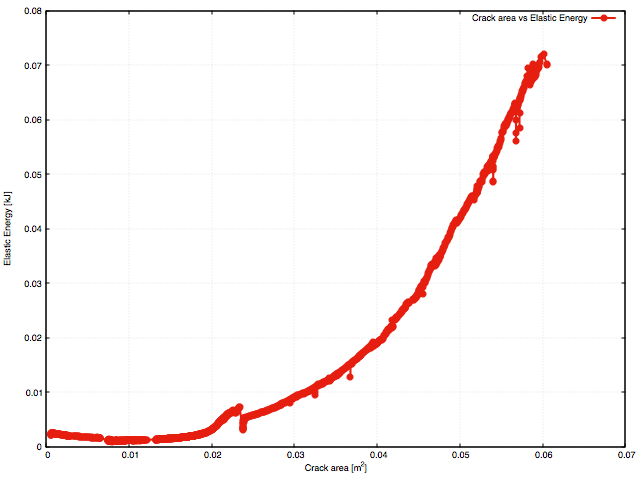
Studying the load-displacement path, it can be noted that it reflects the propagatin of the complex crack path, where initially the crack is unstable. Next on the graphs it can be seen snap-back point, before crack front reaches the end of the keyway. From this point, crack propagation is conditionally stable. At the point where the crack front passing through the end of the keyway, a clear jump is visible on the load-displacement path. It can be noted that before and after that point, the tangent operator is positive and further increase of crack area demands increase of the loading force, i.e. crack propagation is stable. As a result, snap-through is possible, which can be interpreted as the loaded brick will partially break, and crack propagation will freeze if constant ultimate load is applied (assuming that inertia effects are neglected).
The above analyses show the predictive capability of the MoFEM crack modelling technique, allowing for better understanding of crack propagation, delivering not only crack topology but also insight into stability of the crack propagation. This will enable better judgment about safety of component under considered loading.
This test was run with the same command as in previous examples. Input mesh model is generated from the journal file shown below.
The long brick model has a modified geometry at the end of loaded keyway, to enable smooth transfer from a crack propagating along an edge to a crack propagating on the free outer surface. This simplification of the geometry is not expected to change final crack path; however, in the future, alternative options could be considered, both by different model with denser mesh and a dedicated algorithm for resolving such geometrical singularities.
Overall MoFEM performed the tests very successfully. The results showed sensitivity to the applied boundary conditions, showing differences between tests, in particular when the type of loading is changed. This demonstrates the predictive capability. MoFEM is able to deliver information about the crack surface, crack front propagation and load-displacements path, that enables engineers greater interpretation and safety and risk assessment.
Some of key future developments in the context of presented results are listed below;
The ongoing developments are implemented to improve code robustness and reduce direct user time required to set up and run the problem.
This work was supported by the EDF Energy Nuclear Generation Ltd. The views expressed in this paper those of the authors and not necessarily those of the EDF Energy Nuclear Generation Ltd.
