 |
v0.14.0 |
 |
v0.14.0 |
In this tutorial, we show how to solve nonlinear Poisson equation. Note that structure of the main program remains almost unchanged compared to linear analysis as shown in the first Poisson tutorial, i.e. COR-2: Solving the Poisson equation.
As a model problem for the solution of nonlinear PDEs, we take the following nonlinear Poisson equation:
\[ -\nabla \cdot (A(u)\nabla u) = f \]
in domain \(\Omega\) with \(u=\overline{u}\) on boundary \(\partial\Omega\). The source of nonlinearity is the coefficient \(A(u)\) which is dependent on the solution \(u\), here we restrict ourself to the case
\[ A(u) = 1+u^2 \]
Note, code implementation is general, and you can look at the alternative cases, at the beginning of analytical_nonlinear_poisson.cpp example you can find two classes. Those functions can be modified to investigate alternative solutions
Note that second class has to be the exact derivative of \(A(u)\).
With that at hand we can express equation in the weak form, where residuals are
\[ \mathbf{r}= \left[ \begin{array}{c} r_F\\ r_g \end{array} \right]= \left\{ \begin{array}{l} (\nabla v,(1+u^2)\nabla u)_\Omega-(v,f)_\Omega+(v,\lambda)_{\partial\Omega} = 0\\ (\tau,u-\overline{u})_{\partial\Omega} = 0 \end{array} \right.,\quad \forall v,\tau,\; u,v \in H^1(\Omega),\;\tau,\lambda \in H^1(\partial\Omega). \]
where \(\overline{u}\) is given function on boundary, \(f\) is a source term, \(u,\lambda\) are unknown functions and \(v,\tau\) are test functions. This notation, suitable for problems with many terms in the variational formulations, requires some explanation. First, we use the shorthand notation
\[ (v,u)_\Omega = \int_\Omega vu \textrm{d}\Omega,\quad (\lambda,u)_{\partial\Omega} = \int_{\partial \Omega} \lambda u \textrm{d}\partial\Omega \]
With that at hand, we expand residuals in Taylor series and truncate after first order term, as a result we have
\[ \mathbf{r}^i + \frac{\partial \mathbf{r}^i}{\partial \{ u, \lambda \}} \left\{ \begin{array}{c} \delta u^{i+1}\\ \delta \lambda^{i+1} \end{array} \right\} = \mathbf{0} \]
where \((\cdot)^i\) is quantity at Newton iteration \(i\), \(u^{i+1} = u^i + \delta u^{i+1}\) and \(\lambda^{i+1} = \lambda^i + \delta \lambda^{i+1}\). The linearized system of equations takes form
\[ \left\{ \begin{array}{l} r^i_F + (\nabla v,(1+(u^i)^2)\nabla \delta u)_\Omega+(\nabla v,(2u^i) \nabla u^i \delta u^{i+1})_\Omega+(v,\delta\lambda^{i+1}) = 0 \\ r^i_g+ (\tau,\delta u^{i+1})_{\partial\Omega}=0 \end{array} \right. \]
and applying discretization
\[ u^h = \sum_i^{n_u} \phi^i(\mathbf{x}) U_i = \boldsymbol\phi\cdot\mathbf{U} , \quad \mathbf{x} \in \Omega,\\ \lambda^h = \sum_i^{n_\lambda} \psi^i(\mathbf{x}) L_i = \boldsymbol\psi\cdot\mathbf{L} , \quad \mathbf{x} \in \partial\Omega \]
we get
\[ \left[ \begin{array}{c} \mathbf{r}_F\\ \mathbf{r}_g \end{array} \right]+ \left[ \begin{array}{cc} \mathbf{K}_t & \mathbf{C}^T \\ \mathbf{C} & \mathbf{0} \end{array} \right] \left\{ \begin{array}{c} \delta\mathbf{U}^{i+1}\\ \delta\mathbf{L}^{i+1} \end{array} \right\} = \left[ \begin{array}{c} \mathbf{0}\\ \mathbf{0} \end{array} \right] \]
where
\[ \mathbf{K}_t = \int_\Omega (\nabla \boldsymbol\phi)^\textrm{T} (1+(u^i)^2)\nabla \boldsymbol\phi + (\nabla \boldsymbol\phi)^\textrm{T} (2(u^i))\boldsymbol u^i \boldsymbol\phi \textrm{d}\Omega,\\ \mathbf{C} = \int_{\partial\Omega} \boldsymbol\psi^\textrm{T} \boldsymbol\phi \textrm{d}\partial\Omega,\\ \mathbf{r}_F = \mathbf{r}_{F_\Omega} + \mathbf{r}_{F_{\partial\Omega}} = \int_\Omega (\nabla \boldsymbol\phi)^\textrm{T} (1+(u^i)^2)\nabla \boldsymbol u^i - \boldsymbol\phi^\textrm{T}f \textrm{d}\Omega+ \int_{\partial\Omega} \boldsymbol\phi^\textrm{T} \lambda^i \textrm{d}\partial\Omega\\ \mathbf{r}_g = \int_{\partial\Omega} \boldsymbol\psi^\textrm{T} (u^i-\overline{u}) \textrm{d}\partial\Omega \]
To validate correctness of implementation, we first presume exact solution to be polynomial, such that it can be precisely represented by finite element approximation base, see function
where the gradient of that function is implemented here
and source term
Note that source term has a complex form and is obtained from the following formula
\[ f = \nabla \cdot \left( A(u)\nabla u \right) \]
For 3rd polynomial order, as above, results can be obtained after tedious calculations, to avoid that you can use symbolic derivations from Mathematica, Maple, Matlab or free and open alternative Maxima.
All operators from this example are implemented in PoissonOperators.cpp. In particular integration is implemented in the following methods
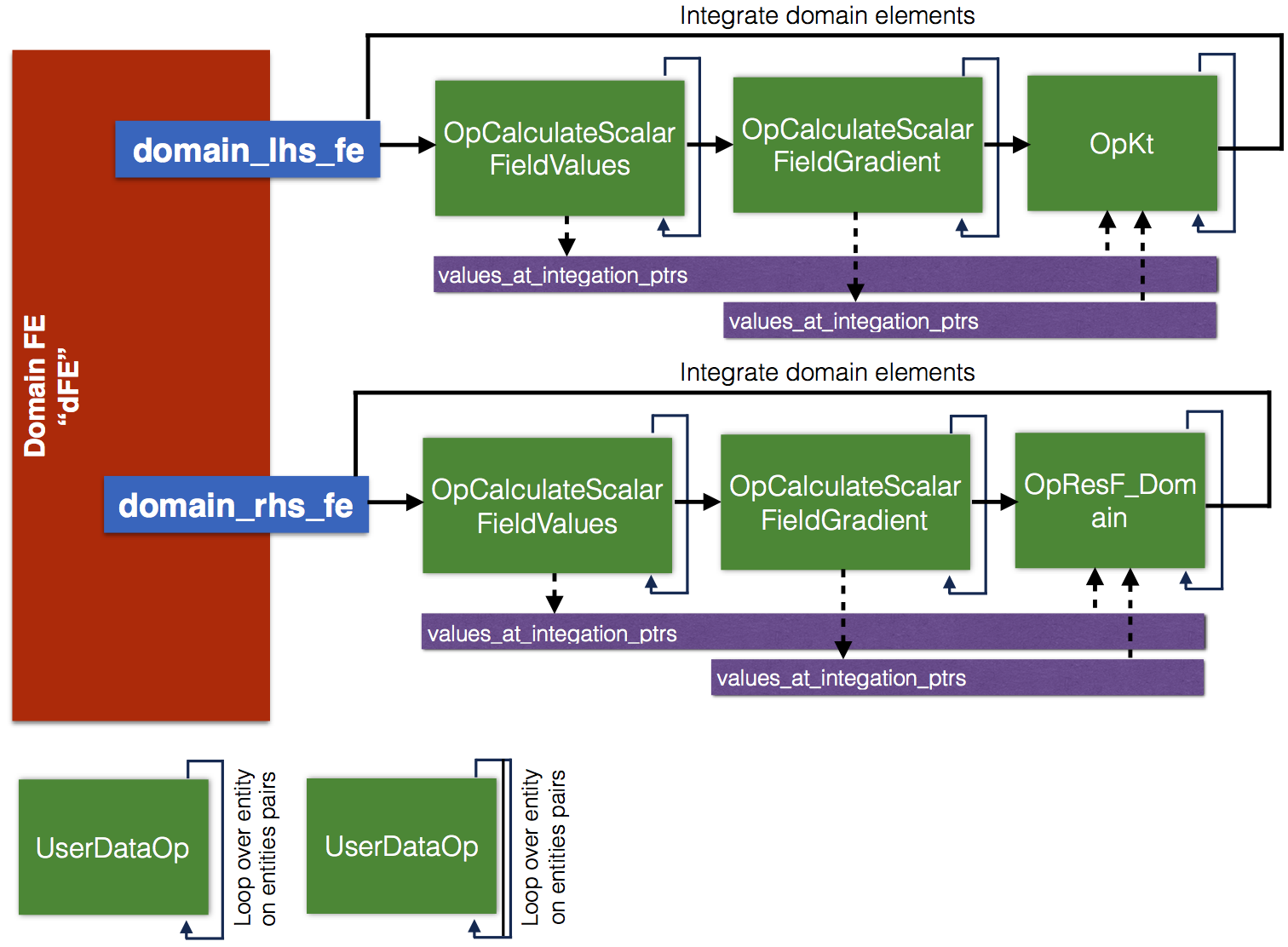
Finite element instances and setup of finite element operators, following Figure 1, is implanted in PoissonExample::CreateFiniteElements::createFEToAssembleMatrixAndVectorForNonlinearProblem, in particular we find there the following code
You can note that instances of vector and matrix are created to store values of function \(u^h\) and function gradients at integration points, respectively. Next operators are added to evaluate function and function gradients at integration points. Finally, operator to calculate tangent matrix is added. Operator constructor takes arguments of pointers of previously created instances of vector and matrix. The same procedure is applied to evaluate residuals by integration over domain and boundary.
Following code is practically the same which we used to linear Poisson example. In nonlinear case, instead of KSP solver, we set-up SNES solver, first by adding finite elements instances to MoFEM SNES solver context
Once we have done this, we create solver instance and kick-start calculations
Note that SNES solver controls DM, and implicitly query of DM to create necessary matrices and assembly of the tangent matrix and residual vectors. SNES solver can be configured from a command line, see for details.
In order to run the program, one should first go to the directory where the problem is located, compile the code and then run the executable file. Typically, this can be done as follows
where SNES options are explained here.
As a result of above command, we get
0 SNES Function norm 6.585598470492e-01
0 KSP Residual norm 6.585598470492e-01
1 KSP Residual norm 5.914941314228e-15
Line search: lambdas = [1., 0.], ftys = [-3.52513, -12.2419]
Line search terminated: lambda = 0.595591, fnorms = 0.34441
1 SNES Function norm 3.444100959814e-01
0 KSP Residual norm 3.444100959814e-01
1 KSP Residual norm 4.038504742986e-15
Line search: lambdas = [1., 0.], ftys = [-0.443111, -2.89313]
Line search terminated: lambda = 0.81914, fnorms = 0.160021
2 SNES Function norm 1.600212778450e-01
0 KSP Residual norm 1.600212778450e-01
1 KSP Residual norm 1.468413895487e-15
Line search: lambdas = [1., 0.], ftys = [-0.00392301, -0.184194]
Line search terminated: lambda = 0.978238, fnorms = 0.0159661
3 SNES Function norm 1.596606319710e-02
0 KSP Residual norm 1.596606319710e-02
1 KSP Residual norm 4.135944054060e-17
Line search: lambdas = [1., 0.], ftys = [-2.21812e-07, -0.000140473]
Line search terminated: lambda = 0.998418, fnorms = 2.23868e-05
4 SNES Function norm 2.238684200528e-05
0 KSP Residual norm 2.238684200528e-05
1 KSP Residual norm 7.619868739966e-20
Line search: lambdas = [1., 0.], ftys = [-4.35284e-16, -4.97174e-10]
Line search terminated: lambda = 0.999999, fnorms = 4.34694e-11
5 SNES Function norm 4.346943842203e-11
Nonlinear solve converged due to CONVERGED_FNORM_RELATIVE iterations 5
Approximation error 4.109e-10
Note fast convergence, after first two interactions, once iterative approximation approaches the exact solution. To obtain this solution, we are using Newton method with line-searcher, in this case, we use critical point secant line search, see details Line-search method has several alternative types and can be setup independently from solver, they can be found here.
