 |
v0.14.0 |
 |
v0.14.0 |
In this tutorial, we focus only on setting up finite element and implementation of user data operator for the Poisson equation. It is the next step after tutorial COR-2: Solving the Poisson equation. Source for this tutorial is in PoissonOperators.hpp.
MoFEM is designed to work with various approximation spaces and is utilizing hierarchical and heterogenous approximation bases. MoFEM design is reflected in hierarchy of classes and implementation of finite elements. Here we introduce user data operators which provide core functionality for application developers.
We distinguish between finite element structure (FES), finite element entity (FEE), finite element class (FEC) and finite element object (FEO);
Implementation of finite element class (FEC) is generic, does not depend on problem or PDE which is solved. The most generic FEC is derived directly from MoFEM::FEMethod. This element delivers raw access to multi-index structures on FEE, enabling to make various queries about DOFs, for example to iterate over DOFs on lower entity of specific type or DOFs associated with particular field and order, utilizing flexibility of multi-index containers. The MoFEM::ForcesAndSourcesCore finite element is derived form MoFEM::FEMethod. From MoFEM::ForcesAndSourcesCore are derived range of elements associated with particular dimensions, MoFEM::VolumeElementForcesAndSourcesCore, MoFEM::FaceElementForcesAndSourcesCore and more or special elements for particular type of entity, e.g. MoFEM::FatPrismElementForcesAndSourcesCore. The MoFEM::ForcesAndSourcesCore provides simplified interface to access DOFs indices, calculation of base functions and other methods specific to finite element entity dimension or finite element entity type. Above comments and insight are not needed to develop application in MoFEM. However, it could help to understand unique capabilities. If you feel confused by the number of names, don't worry, I would be confused on the first reading as well.
Using MoFEM::Simple interface to FES structures are created, for managing elements in domain and boundary. All FEOs are created using FEC derived from MoFEM::VolumeElementForcesAndSourcesCore and MoFEM::FaceElementForcesAndSourcesCore, for domain elements and boundary elements, respectively.
The core functionality of domain finite element instances and boundary element instances are provided by MoFEM::ForcesAndSourcesCore. Application developer do not reimplement finite element, instead provides user data operators (UDO). While implementing finite element method, we can recognize outer loop over FEE, inner loop over lower dimension entities (LDE) on element, and finally most inner loop over base functions on entities and integration points. Application developer focusses his attention on most inner loops, where the physical equations of the problem are implemented. Whereas outer loops on FEE and LDE are managed internally by MoFEM. For example, UDO can be used to integrate bilinear form (calculate elements of matrices) and linear form (elements of the right hand vector).
UDO can be understood as an operator which executes job executed on FEE. UDO are added/pushed to the FEO and called in sequence (order in which are pushed to finite element instance). For example, for vector or matrix assembly, finite elements entity (FEE) are iterated, then FEO is called for FEE. FEO gets data from the database about FEE, calculates base functions on integration points and other bookkeeping operations. FEO iterates over LDE and for each call sequence of UDO.
Hierarchy of UDO classes reflects hierarchy of FEC, where MoFEM::ForcesAndSourcesCore::UserDataOperator is derived from MoFEM::DataOperator. MoFEM::DataOperator is used by core library developers to do low level tasks on element, e.g. applying Piola Transform to base functions, etc. When application developer uses exclusively MoFEM::ForcesAndSourcesCore::UserDataOperator to implement his problem, then implementation is dimension independent. If dimension specific functionality, like recalculated volume of element, or normal of face is needed, then derived user operators can be used, e.g. MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator, MoFEM::FaceElementForcesAndSourcesCore::UserDataOperator and more, see Forces and sources.
In this tutorial, we start with an example of creating finite element instances, i.e. FEO. This is a procedure which is repeated practically for every type of PDE in very similar way. We are using smart pointers to allocate FEO and UDO. If you are not familiar with this C++ technology, you can skip that part and jump into section about the implementation of UDO (see Implementation of user data operators), and come back to the following section later.
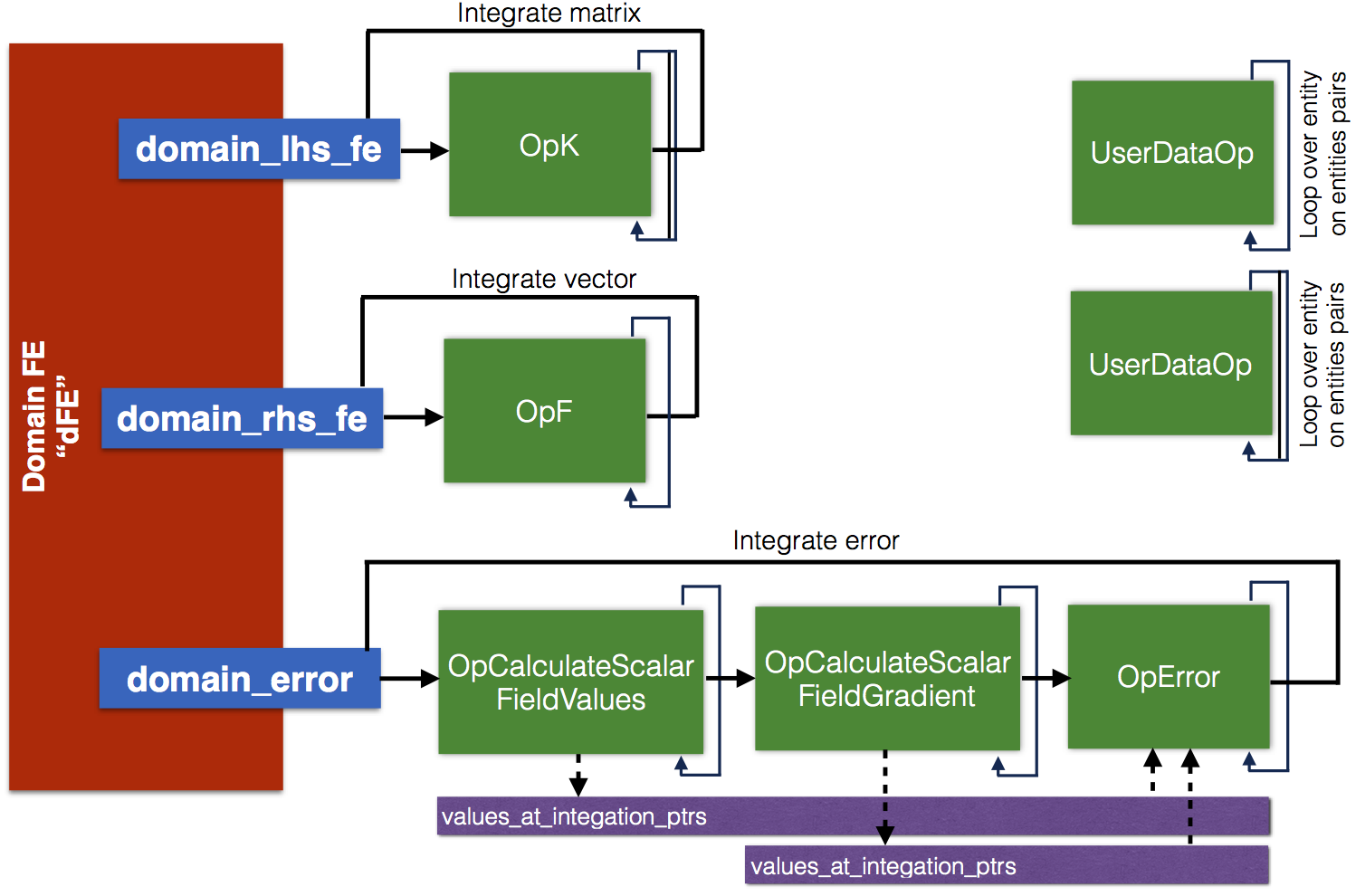
In this example, we are using three finite element instances to integrate fields in domain, i.e. domain_lhs_fe, domain_rhs_fe and domain_error, to integrate matrix, the right-hand vector and error. Implementation of those finite elements is exactly the same, but different operators are added to those elements. For first two: domain_lhs_fe and domain_rhs_fe, only one operator is on the finite element. For domain_error three operators are run in sequence as shown in Figure 1.
To integrate fields on body surface, we have two finite element instances, boundary_lhs_fe and boundary_rhs_fe, see Figure 2.
Setup of all elements used in the Poisson equation example is implemented in the class PoissonExample::CreateFiniteElements, here we focus attention on finite element setup for calculation of matrices and vectors, i.e. PoissonExample::CreateFiniteElements::createFEToAssembleMatrixAndVector.
We will dissect code in PoissonExample::CreateFiniteElements::createFEToAssembleMatrixAndVector
In the first line, we allocate finite element instances
and similarly for other elements. We have smart pointer of type MoFEM::ForcesAndSourcesCore, however allocated finite element instance is type of MoFEM::VolumeElementForcesAndSourcesCore. MoFEM::ForcesAndSourcesCore provides functionality to manage UDO. MoFEM::VolumeElementForcesAndSourcesCore in addition manages complexities associated with integration of volume elements. Using that class, developer is freed from the need of setting integration rule or calling functions to calculate approximation base on entities. Note for boundary elements, appropriately allocated instance is type of MoFEM::FaceElementForcesAndSourcesCore.
Once we have instances of finite element created, we need to choose quadrature rule. For example to integrate term
\[ \mathbf{K}=\int_\Omega \nabla \boldsymbol\phi \cdot \nabla \boldsymbol\phi \textrm{d}\Omega \]
where \(\boldsymbol\phi\) is a base function of polynomial order \(p\), then the integrated term will be the order of \(2(p-1)\), for term in the integral above. To set integrate rule we implement function
Function above for given polynomial order \(p\) return rank \(r=2(p-1)\) which can integrate exactly polynomial order \(p=2r+1\). Integration rule is set to finite element instances as follows
Now we add user data operators to finite element
Dissecting the line, first we start with explicit code
You can see now getOpPtrVector returns vector of pointers to operators acting on finite element lower dimension entities. Now, having vector of pointers, we are going to push operator at the end of it
More interesting case is what happens in PoissonExample::CreateFiniteElements::createFEToEvaluateError, we have, see Figure 1, domain_error finite element instance
Dissecting above code, we start with creating matrix and vector and shared pointers to them so that passed to operators are not destroyed with the end of the scope of the function. Matrix and vector will be destroyed at the time when operators using them are destroyed. Smart pointer will do for us that job and we do not have to think about that any more. Next, we create operator MoFEM::OpCalculateScalarFieldValues, it is one of the standard operators used in various implementations. It calculates field values at integration points and store those values in values_at_integation_ptr. The second operator, i.e. MoFEM::OpCalculateScalarFieldGradient is standard operator to calculate field gradients and store them in grad_at_integation_ptr. Classes MoFEM::OpCalculateScalarFieldValues and MoFEM::OpCalculateScalarFieldGradient are derived from MoFEM::ForcesAndSourcesCore::UserDataOperator and can be used with volume and face elements. Once we have field values and field gradients, we create third operator PoissonExample::OpError, which takes arguments with pointers to exact function, exact function derivatives, and field gradients. With those data at hand, it calculates H1 error norm. Class PoissonExample::OpError is derived form MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator and incense of it can be added only to object of MoFEM::VolumeElementForcesAndSourcesCore.
Let's start with implementation grad-grad operator
User data operator class PoissonExample::OpK is derived from class MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator, which is a generic class to work on 3d finite element entities. Class MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator delivers methods to get the volume of finite element and give access to the data structure of the 3d element and to its quadrature points, etc.
Constructor of operator is
User data operator is used to calculate bilinear form, discrete version of it, i.e. matrix
\[ \mathbf{K} = b(\boldsymbol\phi ,\boldsymbol\phi ) = (\nabla \boldsymbol\phi ,\nabla \boldsymbol\phi)_\Omega = \int_\Omega \nabla \boldsymbol\phi \cdot \nabla \boldsymbol\phi \textrm{d}\Omega \]
The bilinear form takes two function arguments, which on discrete representation are reflected by the scalar product of base function on rows and columns, in this case. That is why we specify field name for row and column, which in this case is the same, i.e. "U". Moreover, since we integrate bilinear form, we set type of operator to OPROWCOL, which indicates that we iterate over unique combination of lower dimension entities on finite element. In our case field "U" is in the H1 space and for tetrahedra, we would iterate over entities
\[ \mathcal{E}_\textrm{row},\mathcal{E}_\textrm{col} = \{VERTICES,EDGES \times 6,TRIAGLES \times 4,TETRAHEDRA \} \]
and we have set of unique pairs,
\[ \begin{array}{l} \mathcal{S} = \{ \left(VERTICES,VERTICES\right), \left(VERTICES,EDGE_0\right),\dots \left(VERTICES,TRIANGLE_0\right),\dots \left(VERTICES,TETRAHEDRA\right),\\ \left(EDGE_0,TRIANGLE_0\right),\dots \left(TRIANGLE_0,TETRAHEDRA\right),\dots \left(TETRAHEDRA,TETRAHEDRA\right) \} \end{array} \]
The number of base functions on each of entities depends on approximation order and space, for example, see how it works for H-div and L2 space here Assembling matrix. Since the last argument in the constructor is "true", it indicates that bilinear form is symmetric and iteration over entities is only for unique unordered pairs, i.e. pair is a set with two elements. The task of integration over entities is managed by MoFEM::ForcesAndSourcesCore finite element from which all entity finite elements are derived.
Now we can dissect overloaded function
This is a virtual function from MoFEM::ForcesAndSourcesCore is executed by finite element while iterating over lower dimension entities. As an argument passes a reference to data structures on rows and columns. Data structure MoFEM::EntitiesFieldData::EntData gives user access DOFs indices and base functions. First, we check if we have DOFs on given entity
if not, we exit the function. Next we get the number of integration points
and check if local entity matrix is on diagonal
This is when a type of entity and its side number (local index of the entity on the finite element) are both the same. Once we have this generic information, we call function to integrate local entity matrix and assemble results to global matrix
The PoissonExample::OpK::iNtegrate method
We can note that first the size of a local matrix is set, then a volume of finite element obtained, next, we get integration weight and gradient of base functions. Finally, we iterate over integration points
We are using Tensor template library here, to iterate over weights and base functions. The essential part of this function is
where the grad-grad term is added to the local matrix.
Finally, we assemble local matrix using PoissonExample::OpK::aSsemble
where the symmetry of the matrix is exploited.
The right-hand operator is constructed first by making a generic class, see PoissonExample::OpBaseRhs. It is a template class with very exact structure to one shown for the grad-grad operator. However, is constructed differently
where OPBASE is a template and is replaced by VolumeElementForcesAndSourcesCore::UserDataOperator or FaceElementForcesAndSourcesCore::UserDataOperator when we integrate source term or constraints, respectively. It takes only argument field_name, which can be "U" or "L" for integration over domain and boundary, respectively. This operator is type OPROW, that means its iterator is over entities
\[ \mathcal{E}_\textrm{row},\mathcal{E}_\textrm{col} = \{VERTICES,EDGES \times 6,TRIAGLES \times 4,TETRAHEDRA \} \]
Another element is an overloaded PoissonExample::OpBaseRhs::doWork function
which has similar for loop to one shown for the grad-grad operator, however, this time base functions and indices are needed on rows only.
With generic operator PoissonExample::OpBaseRhs, we can construct operator for the integration of source term
The constructor of this operator takes as an argument pointer to function where Laplacian is defined. Then the local right-hand side vector is integrated
and assembled
A similar approach is applied to integrate terms associated with Lagrange multipliers. The key advantage of the presented approach is that a difficult problem is broken into small parts, which can be tested and reused for different problems and contexts.
The error operator is derived from PoissonExample::OpBaseRhs class. Here we will focus on PoissonExample::OpError::iNtegrate and PoissonExample::OpError::aSsemble. PoissonExample::OpError is third in sequence. First function values and function gradient are calculated for integration points using MoFEM::OpCalculateScalarFieldValues and MoFEM::OpCalculateScalarFieldGradient respectively. MoFEM::OpCalculateScalarFieldValues and MoFEM::OpCalculateScalarFieldGradient use operators which you find in other examples, and can be used in the context of volume, face, edge and vertex elements.
Constructor of PoissonExample::OpError is as follows
Note that it takes a function pointer to evaluate exact function values and function gradient at integration points. Next, approximate function values and gradients, in shared pointer to vector and matrix, respectively. At last, PETSc vector is taken to accumulate values from all processes.
This operator is type OPROW, and is evaluated for ERROR field which is in L2 space, as results this operator is executed only for set of entities
\[ \mathcal{E}_\textrm{row} = \{ TETRAHEDRA \} \]
with one element only, i.e. TETRAHEDRA.
To integrate error, we have the following code
Note how we get approximate values at integration points. First, we get tensors of rank 0 and rank 1, for field values and gradients, respectively
and then iterate over integration points
using ++t_u and ++t_grad to move tensors to the next integration point. In similar way, coordinates of integration points are iterated. Functions MoFEM::getFTensor0FromVec and MoFEM::getFTensor1FromMat take vector or matrix as an argument and express it using tensor data structure. Function MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator::getFTensor0IntegrationWeight and MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator::getFTensor1CoordsAtGaussPts are overloaded function for volume operator, to get integration weight and coordinates respectively. See MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator for available functions from volume operator.
Next, we accumulate error for all elements and processors
the line
set values to MoFEM database on ERROR field dofs. Next we assemble contributor to global error vector
