 |
v0.14.0 |
 |
v0.14.0 |
Example of implementation, step by step tutorial
This documents assumes that reader is familiar with hierarchical approximation spaces, if not pleas look into paper [1]. In such approximation degrees of freedom are not only associated with vertices but edges and other two- and three- dimensional entities. MoFEM exploit that property and use it as a tool to make efficient and well structured code.
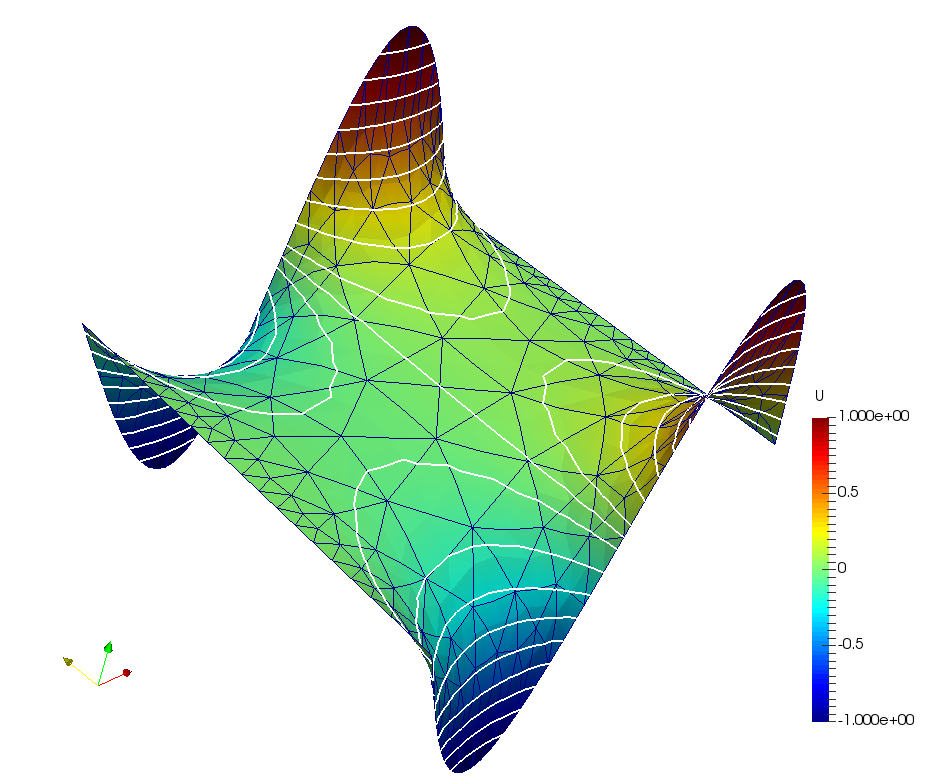
This problem formulation follows tutorial from deal.II https://www.dealii.org/developer/doxygen/deal.II/step_15.html. This problem describe the surface spanned by soap film enclosed between a rigid wire. For simplicity shape of a wire is given by curve \(z=g(x,y)\).
Problem equation in the strong form is given by
\[ -\nabla \cdot \left( \frac{1}{\sqrt{1+\|u\|^2}}\nabla u \right) = 0 \; \textrm{in}\,\Omega,\\ u = g(x,y) \; \textrm{on}\,\partial\Omega \]
Above equation is linearized and applying standard procedure of integration by parts expressed finally in the week form
\[ \int_\Omega \nabla \phi \cdot \left\{ a_i \nabla \delta u_{i+1} - a_i^3 \nabla u_i \cdot \nabla \delta u_{i+1} \nabla u_i \right\} \textrm{d}\Omega + \int_\Omega \nabla \phi \cdot \left\{ a_i \nabla u_{i+1} \right\} \textrm{d}\Omega = 0 \]
where
\[ a_i = \frac{1}{\sqrt{1+\|u_i\|^2}} \]
and \(i\) is iteration number where function values at step \(s\) are updated us follows
\[ u^{s+1} = u^s + \Delta u_{i+1},\\ \Delta u_{i+1} = \Delta u_i + \delta u_{i+1}. \]
MoFEM module (like MatLab toolkit) is independent implementation, which own repository, different owners and license. Adding module is straightforward, CMake search in subdirectories for a file InstalledAddModule.cmake, directory in which such file is placed become an user module. You can look to the How to add user module? for additional information about module installation and its directory structure.
It is good practice that each module has tests verifying correctness of the installation. Having tests is essential for code development and ensures compatibility of a module which MoFEM library and other modules.
The minimal surface problem is implemented as a stand alone independent module which own repository and GNU Lesser General Public License. A module is installed from Bitbucket repository (https://bitbucket.org/likask/mofem_um_minimal_surface_equation) by command,
Modules is compiled with commands
Finally installation is tested with
Since modules are located in different independent repositories, for connivence update of all installed modules is automatized. You can do that with line command;
you can as well update individual module, for example
Alternatively to update this module you can simply do;
In MoFEM like in programming languages like C++ we use declarations, definitions and implementation. A definition of finite element is what MoFEM needs to build data structures in order to make vectors, matrices and set up solvers. A implementation of finite element is what MoFEM needs to do calculations, i.e. calculate element matrices and vectors. Such approach allow to have the same declaration but several definitions (implementations) of the same element.
In this problem we have only one scalar field of a soap surface displacements in \(z\) direction. To solve problem using week form shown above we demand that approximation field belongs to H1 space (i.e. conforming approximation). Since problem is 2D, we span that field on triangles, edges and nodes;
Note that initially we set the same approximation order to each entity. However in general approximation order can be heterogenous. Approximation order of vertices is always "1" for H1 space, since for given nodes values uniquely piecewise linear function is given.
If it is needed additional abstraction, the field can carry additional information about its covariant and contravariant base, see MoFEM::CoordSys. We do not need this here, since we work only with one component of displacement field in Cartesian base.
In MoFEM finite element is entity (Vertex, Edge, Triangle, Quad, Tet, Prism ... Meshset), on which we do some calculations, f.e. integrate internal force vector.
Definition of a finite element resembles how we write bilinear form, f.e. problem in the week form is given by general equation
\[ b(v,u;\alpha) = f(v)\;\in\Omega \]
where \(u,v\in\mathcal{V} \subset H_1(\Omega)\) belongs to some finite vector space and \(\alpha = \alpha(x,y) \in L_2(\Omega)\) is some field of coefficients. A testing function (wighting) space, tested (approximated) field and data (coefficient) field on which bilinear form operates, need to be specified when finite element is declared. Note that in general bilinear form can be decomposed on several parts (by introducing several elements) to split complex problem on simpler tasks.
In this example we declaring two elements, one Edge elements used to calculate approximation of function \(u=g(x,y)\) on boundary \(\partial \Omega\), and another on Triangles to formulate main problem of minimal surface equation in \(\Omega\).
The element in film domain is declared as follows
and for boundary elements element is declared in analogically, as follows
In addition we need to set domain of the finite element, it is done by adding entities to the finite element, for MINIMAL_SURFACE_ELEMENT we will use all triangle elements in the root meshset;
For BC_ELEMENT, we will take a skin form triangles to obtain edges on the boundary and add them to the boundary finite element;
Note that dimension of a domain is not explicitly given, it is associated with the type of an entity, in this case we use triangles and edges. However user can do more exotic combinations, mixing different dimensions and do generic element from a meshset. Dimension of a field is implicitly defined not by a finite element, but fields on which it operates and structure MoFEM::CoordSys carried with each field.
The KSP solver, SNES solver or TS solver from PETSc library could be run directly using native MoFEM interface, optionally PETSc Discrete Manager (DM) http://www.mcs.anl.gov/petsc/petsc-current/docs/manualpages/DM/ can be used by MoFEM DM interface, see Distributed mesh manager.
In this example we will solve sequentially two problems, linear problem finding function approximation on the boundary and nonlinear problem on the film domain. First problem is defined as follows;
where bit_level0 declares on which refinement level problem is solved. In principle user can have several problems on different mesh refinements, or problem which spanning on several nested meshes.
Analogically second problem is created as follows;
Once DMs are created for each problem, using PETSc interface http://www.mcs.anl.gov/petsc/petsc-current/docs/manualpages/DM/ we can create vectors and matrices for each of the problems, f.e.
Such implementation make transparent for user how vectors and matrices are created. Since DM is defined for MoFEM problem, problem is composed from set of finite elements and those are using fields, for given space of those fields (L2,H1,Hdiv,Hcurl) and given entities caring those fields, adjacency matrix is uniquely defined.
In MoFEM solution is build "bottom to up", such that fields, approximations, finite elements and their implementation is a problem independent. This enables to use finite element to solve problems, independently on their dimension and number of fields on which those problems operates.
In this example, we exploit this to some extend. The 1d problem is solved first on the edges and then the 2d problem is solved on triangles. Those two problems operates on the same field and since field is independent from problem, data transfer from one to another is effortless.
To solve problem the right hand side vector and the left hand side matrix need to be calculated,
The element implementation is hidden in its object instance minimal_surface_element.feBcEdge, implementation of this class is discussed in following sections. Having vector and matrices assembled system of equations is solved using KSP solver
Once problem is solved, results are stored in MoFEM database, independently from particular problem numeration, partitioning on several processors or refinement level
Solution of a nonlinear problem in MoFEM is as simple as solving linear problem, taking advantage from PETSc functionality. To run SNES solver one need to register finite element object instances responsible for calculation of a tangent matrix and a vector of residuals, this is simply done as follows;
where fix_edges_ents, minimal_surface_element.feRhs and minimal_surface_element.feLhs are particular finite element implementations. Implementation of fix_edges_ents is not discussed here, it is general propose finite element to enforce essential boundary conditions, in this case fixes DOFs on domain boundary. Implementation of minimal_surface_element.feRhs and minimal_surface_element.feLhs is discussed in following sections.
User can add several elements, for each Newton iteration, elements instances are executed in order in which were added (registered) in MoFEM SNES solver. Low level element class is here MoFEM::FEMethod. Usually user not uses directly this class, it implement using set of so called data entity operators as is shown bellow. Such structure allow to break down complex problem on smaller tasks, easy to debug, reuse in different modules and tests and last but not least produce efficient code.
To create nonlinear solver instance, linked to DM, follow code;
Note that type of SNES solver, line searchers, parameters are set from line command, see for details https://www.mcs.anl.gov/petsc/petsc-current/docs/manualpages/SNES/, in particular https://www.mcs.anl.gov/petsc/petsc-current/docs/manualpages/SNES/SNESSetFromOptions.html
Analyzed problem in this example strongly nonlinear it is convenient to apply sub-stepping, as in the following code;
where DMoFEMMeshToLocalVector get values from the field (previously calculated in boundary problem) and stores values in vector T0. This vector is scaled by size step size and added to unknown vector.
A finite element is simply understand here as a object doing some calculations (usually integration) on some domain associated with element entity, f.e. example for edge is a segment emerged in 1d/2d/3d space depending on needed level of abstraction, for triangle is a 2d domain (potential emerged in some higher order dimension space). Low level implementation starts with MoFEM::FEMethod, however here we will implement elements with some "driver" classes which will do some typical work for a user. This section as well introduces concept user data operator (see MoFEM::DataOperator). In this implementation two types of elements are used Edge Element and Face Element.
Finite element operates on one or several fields, where approximation spaces of fields are span on some set of entities, specific for each field space and approximation order. For example, space H1 and order 1, span only on vertices, order 2 span on vertices and edges, order 3 span additionally on faces, and so on. Another example, space Hdiv in 3d, span only on faces and volumes, depending on approximation order.
Managing complexities for hierarchical and heterogenous approximation fields on unstructured meshes could be difficult. MoFEM try to make that easy but yet give maximal flexibility. Inside of each element, MoFEM loops over all entities or all possible combinations, according to canonical element numeration [tautges_moab:2004]. For each looped entity ordered set of operators (implemented by user) is executed, where from operator user get easy access to finite element data and data on specific entity, like shape functions, vales of degrees of freedom, indices and other data more specific to finite element entity type.
Implementation of this problem is in MinimalSurfaceElement.hpp particular in class MinimalSurfaceEquation::MinimalSurfaceElement.
Problem boundary is implemented with the MoFEM::EdgeElementForcesAndSourcesCore, see
where order of appropriate oder of quadrature is set to integrate least square problem
\[ \int_L \mathbf{N}^\textrm{T}\mathbf{N} \textrm{d}L \; \mathbf{u} = \int_L \mathbf{N}^\textrm{T} g(x,y) \textrm{d}L \]
where \(\mathbf{u}\) represents vector of unknown DOFs on boundary of the domain.
The right hand side vector is calculated using instance of
This UserDataOperator is has type OPROW, it means that it operates on fields which are on rows, "left side" of bilinear form. In that class user has access to range of information on different abstraction levels. Importantly here information about numerical integration, finite element edge length or global position of integration points is accessed. Member function doWork is executed of each entity adjacent to finite element, i.e. vertices and edge. If will be need this class could be inherited and virtual function evalFunction overload, to change function on the boundary of the domain.
The left hand side operator is used to calculate stiffness matrix,
This operator has type OPROWCOL, it means that it loops over rows and columns and all possible combinations, taking in account that problem is symmetric. The values of shape functions at integration points are obtained by
where indices of degrees of freedom can be get by
Note that each operator has overload function doWork, depending which variant of a function is overloaded work is done on rows, columns or combinations or possible rows and columns. This member function is run for all adjacent entities to entity of the finite element.
Each finite element keeps vector of smart pointers to user data operators. The vector of smart pointer to operators in this particulate is accessed by
Finally element is composed by adding to it operators,
which can be executed by Discrete Manager;
The minimal surface area is decomposed on several smaller operations. Note that implementation of operator and finite element is independent of the problem and if there will be need, all showed here operators can be reused in different context in to solve different problem.
Implementation starts with data structure (see MinimalSurfaceEquation::MinimalSurfaceElement::CommonData), shared between finite elements and user data operators. It could be understand as small memory pool, used to sharing and data exchange. Is used as well to accumulate results from different entities;
Next we implement a finite element on face entity, in this particular case on triangle
where here only function controlling quadrature rule is overloaded.
The actual work, i.e. integration of residual and tangent matrix, is made by operators. Here we break down work on smaller four task. In first user data operator is implemented to calculate displacement gradient at each integration points;
This is operator of type OPCOL, it is executed on adjacent entities to finite element entity (in this case, triangle element is adjacent to three vertices, three edges and one face). For each finite element loop over entities starts always from lowest possible entity dimension i.e. vertices, this is exploited here to setup common data structure, i.e. to set sizes and clear vectors and matrixes.
Next coefficients in linearized week from are evaluated;
This operator has two variants controlled by variable rhsAndNotLhs, depending if is executed when left or right hand side is calculated, different set of coefficients is needed. Note that coefficients are calculated for given value of gradient already calculated in different data operator.
Once coefficients are calculated residual vector is assembled;
and tangent matrix
Finally when finite element and entity operators are implemented, we add operators to finite elements instances, we do that staring from the right hand side operator
and left hand side operator
Note that general purpose operators MoFEM::OpCalculateJacForFace, OpInvertMatrix, and MoFEM::OpSetInvJacH1ForFace are used to calculate inverse of the Jacobian, and apply it to gradient of shape functions. Those two operators are implemented as a part core MoFEM library and are used in different contexts if needed.
All operators are run in order which are pushed to given element, so that first inverse of the Jacobian is calculated, then transverse of the inverse of the the Jacobian matrix it is applied to gradients of shape functions, next field gradient is calculated, then coefficients and finally residual vector or tangent matrix.
The elements for the right hand side and the left hand side calculations are added to SNES elements using following code;
Running code:
Program minimal_surface_equationa is started using mpirun, where the number of processors is selected to four in above example. The key parameters are order or approximation and number of sub-steps. In addition user can select different types of line-searchers or change SNES solver and select trust method. More details are available in PETSc documentation of SNES solver, see for details http://www.mcs.anl.gov/petsc/petsc-current/docs/manualpages/SNES/SNESSetFromOptions.html.
In this particular example is run for circular wire loop, function on boundary is given by
\[ u = \sin \left[ \pi (x+y) \right],\quad \textrm{on}\,\partial\Omega \]

Mesh file is created with Cubit https://cubit.sandia.gov
If you like to contribute to this module (or MoFEM library), you are very welcome. Pleas feel free to add changes, including improving this documentation. If you like to work and modify this user module, you can fork this repository, make your changes, and do pull request. Contact us cmatgu@googlegroups.com or https://mofem.slack.com/ if you need any help or comments.
This is work in progress and more stuff can be done. You could consider own paper or student project.
Make this documentation better
Error estimator for L2, H1 and H1 semi-norm
Mesh hp-adaptivity (All tools are there, need be used in this example).
Generalization to arbitrary wire curve in 3d space.
Write documentation about mesh bit levels and mesh refining.
Convergence analysis h- vs. p- refinement.
Adaptive time stepping
