COR-7: Mixed formulation for incompressible elasticity

Table of Contents

• Introduction
• Mathematical and finite element formulation
• Input mesh
• Code dissection
  • Initialisation
  • Solving the problem
  • Postprocessing
• Running the program
  • Output dissection
  • Visualisation
• Remark

Introduction

In this tutorial, the MoFEM implemenetation of the mixed formulation for incompressible elasticity problem will be presented. Interested readers are encouraged to have a look at MoFEM Architecture, FUN-2: Hierarchical approximation, FUN-0: Hello world, and COR-2: Solving the Poisson equation to have better ideas how MoFEM works and how a specific problem is implemented in the platform. They may also find this tutorial video helpful.

The remainder of the tutorial is organised as follows. The mathematical and finite element formulation is presented in the next section before the input mesh of the L-shape structure which is used as an example is defined. It is followed by explanation of the source code and then how to run and visualise the results. Remarks on choosing approximation order and its consequence will be discussed at the end of the tutorial.

Mathematical and finite element formulation

A compressible elasticity problem can be formally defined as follows assuming there is no body force.

For given loading \( \bf{f} \), traction \( \bf{t} \), and displacement \( \bf{\bar u} \), find \( \bf{u} \) such that

\[ \begin{align} -{\rm{div}} \boldsymbol{\sigma(u)} &= \boldsymbol{f} \quad \text{in} \quad \Omega, \\ \boldsymbol{u} &= \boldsymbol{\bar u} \quad \text{on} \quad \Gamma_u \subset \partial\Omega, \\ \boldsymbol{\sigma n} &= \boldsymbol{t} \quad \text{on} \quad \Gamma_t \subset \partial\Omega. \end{align} \]

The constitutive equation is given as

\[ \begin{align} \boldsymbol{\sigma} = \lambda \rm{tr}\boldsymbol{(\varepsilon)I} + 2\mu\boldsymbol{\varepsilon}, \end{align} \]

where Lame's constants \( \lambda \) and \( \mu \) are related with Young's modulus \( E \) and Poisson's ratio \( \nu \) as

\[ \begin{align} \lambda &= \frac{{\nu E}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}, \\ \mu &= \frac{E}{{2\left( {1 + \nu } \right)}}. \end{align} \]

The above problem of compressible elasticity can be solved using typical finite element procedure. However, in case of \( \nu=0.5 \), \( \lambda \) becomes infinity implying incompressible state. This causes volumetric locking which makes the approximation converge very slowly or even unable to converge. Therefore, an alternative formulation needs to be considered to bypass this difficulty. This can be done by introducing additional independent unknown called hydrostatic pressure \( p \) where \( p = -\lambda u_{k,k} \). Therefore, the following equation should be added to the formal problem definition presented in Eqs. (1)-(3)

\[ \begin{align} -{\rm{div}} \boldsymbol{u} + \dfrac{1}{\lambda}p &= 0 \quad \text{in} \quad \Omega. \end{align} \]

With two independent unknowns, \( u \) and \( p \), the incompressible elasticity problem is discretised as follows

\[ \begin{align} \left[ {\begin{array}{*{20}{c}} {\bf{K}}&{\bf{G}}\\ {{{\bf{G}}^T}}&{\bf{P}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\bf{ u}}}\\ {{\bf{ p}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\bf{ f}}}\\ {\bf{0}} \end{array}} \right\}, \end{align} \]

where

\[ \begin{align} {\bf{K}} &= \int\limits_\Omega {{{\bf{B}}^T}{{\bf{D}}_d}{\bf{B}}d\Omega } \\ {\bf{G}} &= - \int\limits_\Omega {{{\bf{B}}^T}{\bf m}{{\bf{N}}_p}d\Omega }, \\ {\bf{P}} &= - \int\limits_\Omega {{\bf{N}}_p^T\frac{1}{\lambda }{{\bf{N}}_p}d\Omega }, \\ {\bf{ f}} &= \int\limits_\Gamma {{\bf{N}}_u^T{\bf{t}}d\Gamma }. \end{align} \]

In the platform of MoFEM, while the complete implementation of user data operators (UDO) can be found in elasticity_mixed_formulation.cpp and ElasticityMixedFormulation.hpp, the matrices above are implemented in UDO as follows

• \( {\bf K} \) is implemented in OpAssembleK
• \( {\bf G} \) is implemented in OpAssembleG
• \( {\bf P} \) is implemented in OpAssembleP

It is worth noting that, in order to obtain stable results for the problem of incompressible elasticity, the approximation order of displacement should be higher than that of hydrostatic pressure. The consequences of choosing inappropriate approximation order of the two unknowns will be discussed later in this tutorial.

Input mesh

As an example, an L-shape structure being clamped at the bottom surface and pressurised with unit magnitude at the top right surface will be used for the analysis of incompressible elasticity. The 3D model and mesh which shown in Figure 1 are created by Cubit using a simple journal script below

reset
set duplicate block elements on
 
brick x 1 y 2 z 0.5
brick x 2 y 1 z 0.5
 
move curve 23 midpoint location curve 11 include_merged
unite volume all 
 
Sideset 1 surface 3 
Sideset 2 surface 12 
 
Sideset 100 curve all 
nodeset 101 vertex all 
Sideset 102 surface all
 
{young_modulus = 1}
{poisson_ratio = 0.5}
block 1 volume all 
block 1 name 'MAT_ELASTIC'
block 1 attribute count 2
block 1 attribute index 1 {young_modulus}
block 1 attribute index 2 {poisson_ratio} 
 
create displacement on surface 3 dof 1 dof 2 dof 3 fix 0
create pressure on surface 12 magnitude 1 
 
volume all scheme tetmesh
volume all size auto factor 7
mesh volume all
 
save as "/Users/username/mofem_install/um/build/basic_finite_elements/elasticity_mixed_formulation/LShape_incompressible.cub" overwrite

Figure 1: Element mesh.

Code dissection

Initialisation

• There are two header files in which the first one for basic finite elements and the second one contains the implementation of operators for finite elements.

#include <ElasticityMixedFormulation.hpp>

• Initialise MoFEM

  // Initialise MoFEM
  MoFEM::Core::Initialize(&argc, &argv, (char *)0, help);

• Create mesh database and an interface to interact with it

  // Create mesh database
  moab::Core mb_instance;              // create database
  moab::Interface &moab = mb_instance; // create interface to database

• Creat MoAB communicator

  MPI_Comm moab_comm_world;
  auto moab_comm_wrap =
      boost::make_shared<WrapMPIComm>(PETSC_COMM_WORLD, false);
  if (pcomm == NULL)
    pcomm =
        new ParallelComm(&moab, moab_comm_wrap->get_comm());

• Declare variables and read arguments from the command line

  // Get command line options
      char mesh_file_name[255];
      PetscBool flg_file;
      int order_p = 2; // default approximation order_p
      int order_u = 3; // default approximation order_u
      PetscBool is_partitioned = PETSC_FALSE;
      PetscBool calc_reactions = PETSC_FALSE;
      PetscBool flg_test = PETSC_FALSE; // true check if error is numerical error
   
      CHKERR PetscOptionsBegin(PETSC_COMM_WORLD, "", "Mix elastic problem",
                               "none");
   
      CHKERR PetscOptionsString("-my_file", "mesh file name", "", "mesh.h5m",
                                mesh_file_name, 255, &flg_file);
      // Set approximation order
      CHKERR PetscOptionsInt("-my_order_p", "approximation order_p", "", order_p,
                             &order_p, PETSC_NULL);
      CHKERR PetscOptionsInt("-my_order_u", "approximation order_u", "", order_u,
                             &order_u, PETSC_NULL);
   
      CHKERR PetscOptionsBool("-is_partitioned", "is_partitioned?", "",
                              is_partitioned, &is_partitioned, PETSC_NULL);
      CHKERR PetscOptionsBool("-calc_reactions",
                              "calculate reactions for blocksets", "",
                              calc_reactions, &calc_reactions, PETSC_NULL);
      // Set testing (used by CTest)
      CHKERR PetscOptionsBool("-test", "if true is ctest", "", flg_test,
                              &flg_test, PETSC_NULL);
      ierr = PetscOptionsEnd();
   
      if (flg_file != PETSC_TRUE) {
        SETERRQ(PETSC_COMM_SELF, 1, "*** ERROR -my_file (MESH FILE NEEDED)");
      }

• Read the mesh

  // Read whole mesh or part of it if partitioned
   if (is_partitioned == PETSC_TRUE) {
     // This is a case of distributed mesh and algebra. In that case each
     // processor keeps only part of the problem.
     const char *option;
     option = "PARALLEL=READ_PART;"
              "PARALLEL_RESOLVE_SHARED_ENTS;"
              "PARTITION=PARALLEL_PARTITION;";
     CHKERR moab.load_file(mesh_file_name, 0, option);
   } else {
     // In this case, we have distributed algebra, i.e. assembly of vectors and
     // matrices is in parallel, but whole mesh is stored on all processors.
     // Solver and matrix scales well, however problem set-up of problem is
     // not fully parallel.
     const char *option;
     option = "";
     CHKERR moab.load_file(mesh_file_name, 0, option);
   }

• Creat MoFEM database

  // Create MoFEM database and link it to MoAB
      MoFEM::Core core(moab);
      MoFEM::Interface &m_field = core;

• Output boundary condition and material properties from the mesh

  // Print boundary conditions and material parameters
  MeshsetsManager *meshsets_mng_ptr;
  CHKERR m_field.getInterface(meshsets_mng_ptr);
  CHKERR meshsets_mng_ptr->printDisplacementSet();
  CHKERR meshsets_mng_ptr->printForceSet();
  CHKERR meshsets_mng_ptr->printMaterialsSet();

• Add three fields

  // **** ADD FIELDS **** //
  CHKERR m_field.add_field("MESH_NODE_POSITIONS", H1, AINSWORTH_LEGENDRE_BASE,
                           3);
  CHKERR m_field.add_ents_to_field_by_type(0, MBTET, "MESH_NODE_POSITIONS");
  CHKERR m_field.set_field_order(0, MBVERTEX, "MESH_NODE_POSITIONS", 1);
   
  CHKERR m_field.add_field("U", H1, AINSWORTH_LEGENDRE_BASE, 3);
  CHKERR m_field.add_ents_to_field_by_type(0, MBTET, "U");
  CHKERR m_field.set_field_order(0, MBVERTEX, "U", 1);
  CHKERR m_field.set_field_order(0, MBEDGE, "U", order_u);
  CHKERR m_field.set_field_order(0, MBTRI, "U", order_u);
  CHKERR m_field.set_field_order(0, MBTET, "U", order_u);
   
  CHKERR m_field.add_field("P", H1, AINSWORTH_LEGENDRE_BASE, 1);
  CHKERR m_field.add_ents_to_field_by_type(0, MBTET, "P");
  CHKERR m_field.set_field_order(0, MBVERTEX, "P", 1);
  CHKERR m_field.set_field_order(0, MBEDGE, "P", order_p);
  CHKERR m_field.set_field_order(0, MBTRI, "P", order_p);
  CHKERR m_field.set_field_order(0, MBTET, "P", order_p);

• Build fields

  CHKERR m_field.build_fields();
   
  // CHKERR m_field.getInterface<FieldBlas>()->setField(
  //     0, MBVERTEX, "P"); // initial p = 0 everywhere
  {
    Projection10NodeCoordsOnField ent_method_material(m_field,
                                                      "MESH_NODE_POSITIONS");
    CHKERR m_field.loop_dofs("MESH_NODE_POSITIONS", ent_method_material);
  }

• Add finite elements

  // **** ADD ELEMENTS **** //
  // Add finite element (this defines element, declaration comes later)
  CHKERR m_field.add_finite_element("ELASTIC");
  CHKERR m_field.modify_finite_element_add_field_row("ELASTIC", "U");
  CHKERR m_field.modify_finite_element_add_field_col("ELASTIC", "U");
  CHKERR m_field.modify_finite_element_add_field_data("ELASTIC", "U");
   
  CHKERR m_field.modify_finite_element_add_field_row("ELASTIC", "P");
  CHKERR m_field.modify_finite_element_add_field_col("ELASTIC", "P");
  CHKERR m_field.modify_finite_element_add_field_data("ELASTIC", "P");
  CHKERR m_field.modify_finite_element_add_field_data("ELASTIC",
                                                      "MESH_NODE_POSITIONS");

• Add entities to elements and build them

  // Add entities to that element
   CHKERR m_field.add_ents_to_finite_element_by_type(0, MBTET, "ELASTIC");
   // build finite elements
   CHKERR m_field.build_finite_elements();
   // build adjacencies between elements and degrees of freedom
   CHKERR m_field.build_adjacencies(bit_level0); 

• Build and setup discrete manager

  // **** BUILD DM **** //
  DM dm;
  DMType dm_name = "DM_ELASTIC_MIX";
  // Register DM problem
  CHKERR DMRegister_MoFEM(dm_name);
  CHKERR DMCreate(PETSC_COMM_WORLD, &dm);
  CHKERR DMSetType(dm, dm_name);
  // Create DM instance
  CHKERR DMMoFEMCreateMoFEM(dm, &m_field, dm_name, bit_level0);
  // Configure DM form line command options (DM itself, solvers,
  // pre-conditioners, ... )
  CHKERR DMSetFromOptions(dm);
  // Add elements to dm (only one here)
  CHKERR DMMoFEMAddElement(dm, "ELASTIC");
  if (m_field.check_finite_element("PRESSURE_FE"))
    CHKERR DMMoFEMAddElement(dm, "PRESSURE_FE");
  if (m_field.check_finite_element("FORCE_FE"))
    CHKERR DMMoFEMAddElement(dm, "FORCE_FE");
  CHKERR DMMoFEMSetIsPartitioned(dm, is_partitioned);
  // setup the DM
  CHKERR DMSetUp(dm);

• Declare share pointers to finit element objects

  boost::shared_ptr<FEMethod> nullFE;
  boost::shared_ptr<VolumeElementForcesAndSourcesCore> feLhs(
      new VolumeElementForcesAndSourcesCore(m_field));
  boost::shared_ptr<VolumeElementForcesAndSourcesCore> feRhs(
      new VolumeElementForcesAndSourcesCore(m_field));

Solving the problem

• Stiffness matrix, vector of DOFs, and right-hand-side (RHS) vector are declared and associated to the Discrete Manager

  Mat Aij;      // Stiffness matrix
  Vec d, F_ext; // Vector of DOFs and the RHS
   
  {
    CHKERR DMCreateGlobalVector_MoFEM(dm, &d);
    CHKERR VecZeroEntries(d);
    CHKERR VecDuplicate(d, &F_ext);
    CHKERR DMCreateMatrix_MoFEM(dm, &Aij);
    CHKERR VecGhostUpdateBegin(d, INSERT_VALUES, SCATTER_FORWARD);
    CHKERR VecGhostUpdateEnd(d, INSERT_VALUES, SCATTER_FORWARD);
    CHKERR DMoFEMMeshToLocalVector(dm, d, INSERT_VALUES, SCATTER_REVERSE);
    CHKERR MatZeroEntries(Aij);
  }

• Finite element instances are pointed to the matrix and vector

  // Assign global matrix/vector
  feLhs->ksp_B = Aij;
  feLhs->ksp_f = F_ext;

• Loop over element to compute and assemble stiffness matrix, vectors of DOFs and RHS

  boost::shared_ptr<DirichletDisplacementBc> dirichlet_bc_ptr(
      new DirichletDisplacementBc(m_field, "U", Aij, d, F_ext));
  dirichlet_bc_ptr->snes_ctx = FEMethod::CTX_SNESNONE;
  dirichlet_bc_ptr->ts_ctx = FEMethod::CTX_TSNONE;
  CHKERR DMoFEMPreProcessFiniteElements(dm, dirichlet_bc_ptr.get());
  CHKERR DMoFEMLoopFiniteElements(dm, "ELASTIC", feLhs);
   
  // Assemble pressure and traction forces.
  boost::ptr_map<std::string, NeumannForcesSurface> neumann_forces;
  CHKERR MetaNeumannForces::setMomentumFluxOperators(m_field, neumann_forces,
                                                     F_ext, "U");
   
  {
    boost::ptr_map<std::string, NeumannForcesSurface>::iterator mit =
        neumann_forces.begin();
    for (; mit != neumann_forces.end(); mit++) {
      CHKERR DMoFEMLoopFiniteElements(dm, mit->first.c_str(),
                                      &mit->second->getLoopFe());
    }
  }
  // Assemble forces applied to nodes, see implementation in NodalForce
  boost::ptr_map<std::string, NodalForce> nodal_forces;
  CHKERR MetaNodalForces::setOperators(m_field, nodal_forces, F_ext, "U");
   
  {
    boost::ptr_map<std::string, NodalForce>::iterator fit =
        nodal_forces.begin();
    for (; fit != nodal_forces.end(); fit++) {
      CHKERR DMoFEMLoopFiniteElements(dm, fit->first.c_str(),
                                      &fit->second->getLoopFe());
    }
  }
  // Assemble edge forces
  boost::ptr_map<std::string, EdgeForce> edge_forces;
  CHKERR MetaEdgeForces::setOperators(m_field, edge_forces, F_ext, "U");
   
  {
    boost::ptr_map<std::string, EdgeForce>::iterator fit =
        edge_forces.begin();
    for (; fit != edge_forces.end(); fit++) {
      CHKERR DMoFEMLoopFiniteElements(dm, fit->first.c_str(),
                                      &fit->second->getLoopFe());
    }
  }
   
  CHKERR DMoFEMPostProcessFiniteElements(dm, dirichlet_bc_ptr.get());
  CHKERR DMMoFEMKSPSetComputeOperators(dm, "ELASTIC", feLhs, nullFE, nullFE);
  CHKERR VecAssemblyBegin(F_ext);
  CHKERR VecAssemblyEnd(F_ext);

• The matrix and vectors have been assembled and now the system of equation is solved using KSP solver

  KSP solver;
   
  CHKERR KSPCreate(PETSC_COMM_WORLD, &solver);
  CHKERR KSPSetFromOptions(solver);
  CHKERR KSPSetOperators(solver, Aij, Aij);
  CHKERR KSPSetUp(solver);
  CHKERR KSPSolve(solver, F_ext, d);

• Map the solutions to mesh entities

  CHKERR DMoFEMMeshToGlobalVector(dm, d, INSERT_VALUES, SCATTER_REVERSE);

Postprocessing

• The solutions are passed to the postprocessor and information is written to the output file

  CHKERR post_proc.generateReferenceElementMesh();
  CHKERR post_proc.addFieldValuesPostProc("U");
  CHKERR post_proc.addFieldValuesPostProc("P");
   
  CHKERR DMoFEMLoopFiniteElements(dm, "ELASTIC", &post_proc);
  PetscPrintf(PETSC_COMM_WORLD, "Output file: %s\n", "out.h5m");
  CHKERR post_proc.postProcMesh.write_file("out.h5m", "MOAB",
                                           "PARALLEL=WRITE_PART");

• Finally, all dynamic objects Aij, d, F_ext, and Discrete Manager are destroyed to release memory

  CHKERR MatDestroy(&Aij);
  CHKERR VecDestroy(&d);
  CHKERR VecDestroy(&F_ext);
  CHKERR DMDestroy(&dm);

Running the program

In order to run the program, one should first go to the directory where the problem is located, compile the code and then run the executable file. Typically, this can be done as follows

cd mofem_install/um/build/basic_finite_elements/elasticity_mixed_formulation
make -j2
mpirun -np 2 ./elasticity_mixed_formulation -my_file LShape_incompressible.cub -my_order_p 2 -my_order_u 3 -ksp_type gmres -pc_type lu -pc_factor_mat_solver_type mumps -ksp_monitor

The options are explained as follows

• mpirun -np 2: two processors are used to run the analysis
• ./elasticity_mixed_formulation: path and name of the executable file, dot means current directory
• -my_file LShape_incompressible.cub: name of the mesh file
• -my_order_p 2: second order approximation for hydrostatic pressure p
• -my_order_u 3: third order approximation for displacement u
• -ksp_type gmres: Generalised Minimal Residual is used as an iterative Krylov subspace method
• -pc_type lu: Direct solver based on LU factorisation as a preconditioner
• -pc_factor_mat_solver_type mumps: MUMPS is used as matrix solver
• -ksp_monitor: function to be called at every iteration to monitor the residual/error

Output dissection

Initialisation and Setup

• Cubit mesh being read

  read cubit meshset 12682136550675316776 type BLOCKSET MAT_ELASTICSET msId 1 name MAT_ELASTIC block header:  blockCol = 4294967295 blockMat = 0 blockDimension = 3
  read cubit meshset 12682136550675316777 type NODESET DISPLACEMENTSET msId 1
  read cubit meshset 12682136550675316778 type NODESET msId 101
  read cubit meshset 12682136550675316779 type SIDESET msId 1
  read cubit meshset 12682136550675316780 type SIDESET msId 2
  read cubit meshset 12682136550675316781 type SIDESET PRESSURESET msId 3
  read cubit meshset 12682136550675316782 type SIDESET msId 100
  read cubit meshset 12682136550675316783 type SIDESET msId 102

• MoFEM version and commit ID

  MoFEM version 0.8.15 (MOAB 5.0.2 Petsc Release Version 3.9.3, Jul, 02, 2018 ) 
  git commit id cdfa37ee13d92b014cc527b5ab7b844baf73f98d

• Boundary conditions from the mesh

  D i s p l a c e m e n t 
   
  Flag for X-Translation (0/1): 1
  Flag for Y-Translation (0/1): 1
  Flag for Z-Translation (0/1): 1
  Flag for X-Rotation (0/1): 0
  Flag for Y-Rotation (0/1): 0
  Flag for Z-Rotation (0/1): 0
   
  Displacement magnitude (X-Translation): 0
  Displacement magnitude (Y-Translation): 0
  Displacement magnitude (Z-Translation): 0
  Displacement magnitude (X-Rotation): N/A
  Displacement magnitude (Y-Rotation): N/A
  Displacement magnitude (Z-Rotation): N/A

• Material used in the mesh

  meshset 12682136550675316776 type BLOCKSET MAT_ELASTICSET msId 1 name MAT_ELASTIC block header:  blockCol = 4294967295 blockMat = 0 blockDimension = 3
   
  Material Properties
  -------------------
  Young's modulus  = 1
  Poisson's ratio  = 0.5
  Thermal expansion = 0
  User attribute 1 = 0
  User attribute 2 = 0
  User attribute 3 = 0
  User attribute 4 = 0
  User attribute 5 = 0
  User attribute 6 = 0
  User attribute 7 = 0
   
  MAT_ELATIC msId 1 nb. tets 471

• Three fields are added to the database. Fields are then built showing the number of active degrees of freedom (DOFs) for entities including vertices, edges, triangles (faces).

  add: name MESH_NODE_POSITIONS BitFieldId 1 bit number 1 space H1 approximation base AINSWORTH_LEGENDRE_BASE rank 3 meshset 12682136550675316786
  add: name U BitFieldId 2 bit number 2 space H1 approximation base AINSWORTH_LEGENDRE_BASE rank 3 meshset 12682136550675316787
  add: name P BitFieldId 4 bit number 3 space H1 approximation base
  AINSWORTH_LEGENDRE_BASE rank 1 meshset 12682136550675316788
   
  Build Field MESH_NODE_POSITIONS (rank 0)
  nb added dofs (vertices) 465 (inactive 0)
  nb added dofs 465 (number of inactive dofs 0)
  Build Field U (rank 0)
  nb added dofs (vertices) 465 (inactive 0)
  nb added dofs (edges) 4482 (inactive 0)
  nb added dofs (triangles) 3192 (inactive 0)
  nb added dofs 8139 (number of inactive dofs 0)
  Build Field P (rank 0)
  nb added dofs (vertices) 155 (inactive 0)
  nb added dofs (edges) 747 (inactive 0)
  nb added dofs 902 (number of inactive dofs 0)
  Nb. dofs 9506
  Build Field MESH_NODE_POSITIONS (rank 1)
  nb added dofs (vertices) 465 (inactive 0)
  nb added dofs 465 (number of inactive dofs 0)
  Build Field U (rank 1)
  nb added dofs (vertices) 465 (inactive 0)
  nb added dofs (edges) 4482 (inactive 0)
  nb added dofs (triangles) 3192 (inactive 0)
  nb added dofs 8139 (number of inactive dofs 0)
  Build Field P (rank 1)
  nb added dofs (vertices) 155 (inactive 0)
  nb added dofs (edges) 747 (inactive 0)
  nb added dofs 902 (number of inactive dofs 0)
  Nb. dofs 9506

• Three elements are added to the database. Finite elements are then built.

  add finite element: FORCE_FE
  add finite element: PRESSURE_FE
  add finite element: ELASTIC
   
  Build Finite Elements FORCE_FE
  Build Finite Elements PRESSURE_FE
  Build Finite Elements ELASTIC
  Nb. FEs 485
  Nb. FEs 485
  id 00000000000000000000000000000001 name FORCE_FE f_id_row 00000000000000000000000000000010 f_id_col 00000000000000000000000000000010 BitFEId_data 00000000000000000000000000000011 Nb. FEs 0
  id 00000000000000000000000000000001 name FORCE_FE f_id_row 00000000000000000000000000000010 f_id_col 00000000000000000000000000000010 BitFEId_data 00000000000000000000000000000011 Nb. FEs 0
  id 00000000000000000000000000000010 name PRESSURE_FE f_id_row 00000000000000000000000000000010 f_id_col 00000000000000000000000000000010 BitFEId_data 00000000000000000000000000000011 Nb. FEs 14
  id 00000000000000000000000000000010 name PRESSURE_FE f_id_row 00000000000000000000000000000010 f_id_col 00000000000000000000000000000010 BitFEId_data 00000000000000000000000000000011 Nb. FEs 14
  id 00000000000000000000000000000100 name ELASTIC f_id_row 00000000000000000000000000000110 f_id_col 00000000000000000000000000000110 BitFEId_data 00000000000000000000000000000111 Nb. FEs 471
  id 00000000000000000000000000000100 name ELASTIC f_id_row 00000000000000000000000000000110 f_id_col 00000000000000000000000000000110 BitFEId_data 00000000000000000000000000000111 Nb. FEs 471
  Nb. entFEAdjacencies 13328
  Nb. entFEAdjacencies 13328

• Problem is added and then built

  add problem: DM_ELASTIC_MIX
  Problem DM_ELASTIC_MIX Nb. rows 9041 Nb. cols 9041
  Problem DM_ELASTIC_MIX Nb. rows 9041 Nb. cols 9041
  Partition problem DM_ELASTIC_MIX
      create_Mat: row lower 0 row upper 4521
      create_Mat: row lower 4521 row upper 9041
  partition_problem: rank = 0 FEs row ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. local dof 4653 nb global row dofs 9041
  partition_problem: rank = 0 FEs col ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. local dof 4653 nb global col dofs 9041
  partition_problem: rank = 1 FEs row ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. local dof 4388 nb global row dofs 9041
  partition_problem: rank = 1 FEs col ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. local dof 4388 nb global col dofs 9041
  problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. elems 244 on proc 0
  problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. elems 241 on proc 1
  partition_ghost_col_dofs: rank = 0 FEs col ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. col ghost dof 221 Nb. local dof 4653
  partition_ghost_row_dofs: rank = 0 FEs row ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. row ghost dof 221 Nb. local dof 4653
  partition_ghost_col_dofs: rank = 1 FEs col ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. col ghost dof 181 Nb. local dof 4388
  partition_ghost_row_dofs: rank = 1 FEs row ghost dofs problem id 00000000000000000000000000000001 FiniteElement id 00000000000000000000000000000111 name DM_ELASTIC_MIX Nb. row ghost dof 181 Nb. local dof 4388

Solution

• KSP solver output

  0 KSP Residual norm 2.422191940287e+02 
  1 KSP Residual norm 3.461359964609e-11

• Output file

  Output file: out.h5m

Visualisation

Once the solution is obtained, one can convert the output file which has the extension of h5m to a vtk one before opening it in ParaView.

mbconvert out.h5m out.vtk
open out.vtk

The visualisation of the results can then be viewed as shown in Figure 2 and Figure 3 for displacement and hydrostatic pressure, respectively.

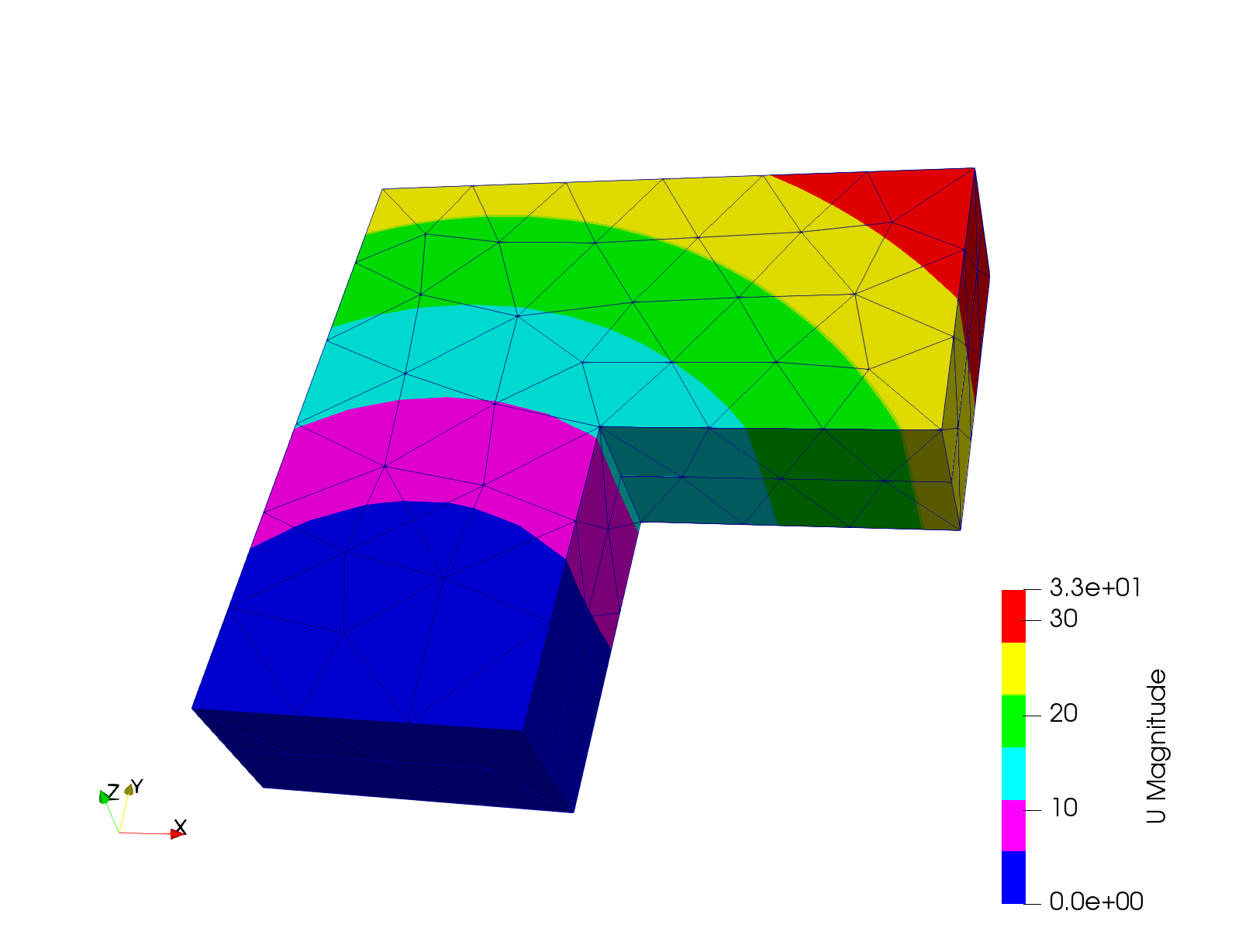
Figure 2: Visualisation of displacement result.

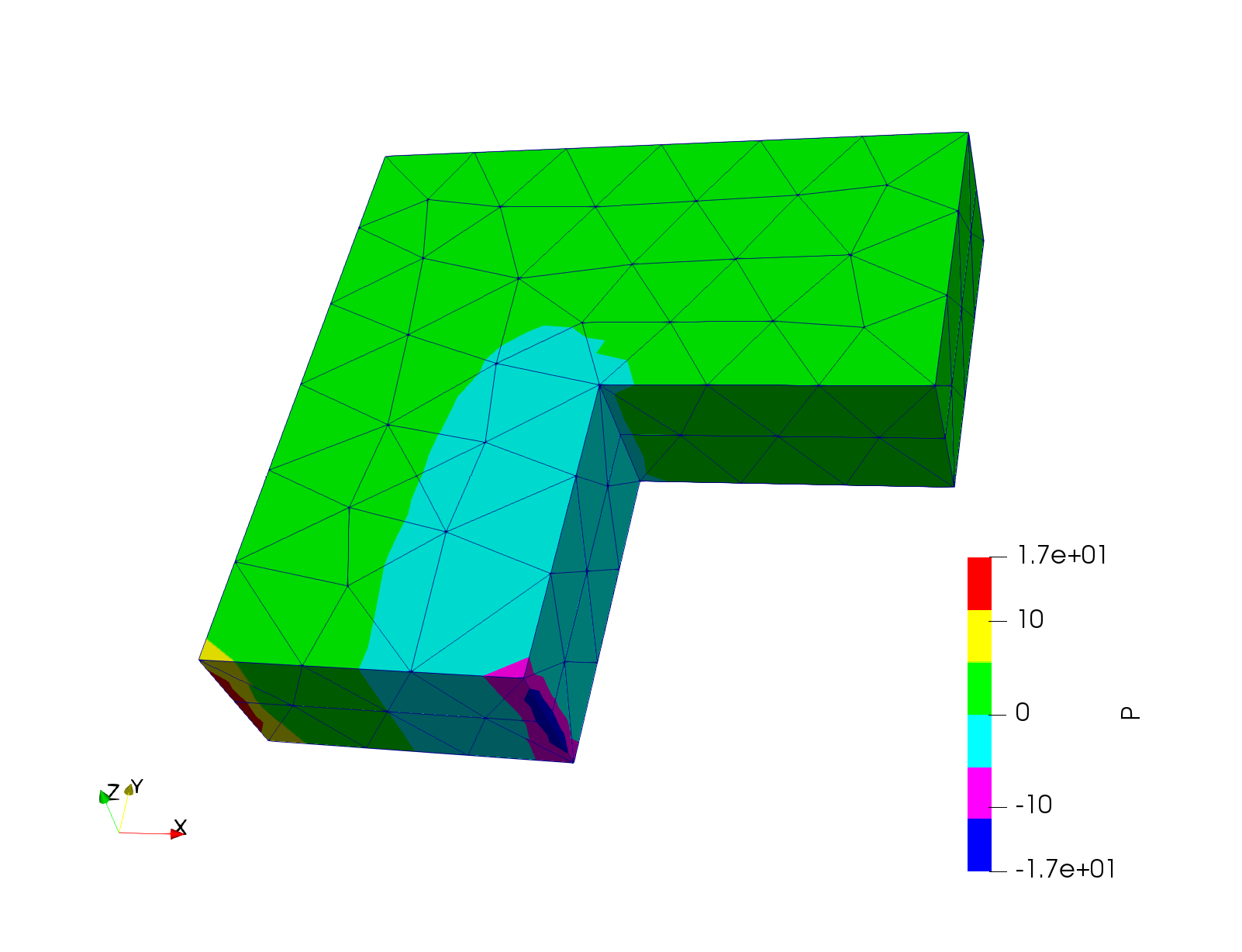
Figure 3: Visualisation of hydrostatic pressure result.

Remark

As mentioned earlier, the choices of approximation order for hydrostatic pressure and displacement are important. Practically, the approximation order of displacement should be higher than that of hydrostatic pressure. If the same order is assigned for displacement and hydrostatic pressure, oscillating results are expected as shown in Figure 4.

Figure 4: Output of hydrostatic pressure when second order approximation is chosen for both variables.