Fisher's reaction-diffusion equation
Fisher's equation [26] describes the population dynamics, transformation of species into "mutant" species in space and time. Its predictive capabilities include modelling of fire propagation, virile mutant propagation, evolution of a neutron population in a nuclear reactor, spreading of Alzheimer's disease in human brain, and many more phenomena.
In this tutorial, we consider the equation in its original form presented by Fisher in 1937 [26]
\[ \frac{\partial u}{\partial t} - D \nabla^2 u = ru\left(1-\frac{u}{k}\right) \]
where \(D\) is diffusivity, \(r\) is rate factor and \(k\) is carrying capacity. This equation can be interpreted that advancing wave with a speed no greater than \(\sqrt{Dr}\) will transform abandoned species into another "mutant" form, switching state variable \(u\) from the equilibrium state of \(u=0\) to another equilibrium state of \(u=k\).
To understand the equation better, we can focus our attention on the spreading of fire on a plane of dry grass which is isolated from the rest of the domain by a closed trench of water. Fire will spread over the whole area, whereby all grass over time will be consumed by fire and transformed into ash, i.e. mutant, where virgin (unburned) grass is indicated by \(u=0\), and grass consumed by fire, i.e. ash is \(u=k\). The front of the fire will move with the velocity not greater than \(\sqrt{Dr}\). In the case with the grass is mixed with a plant having some resistance to fire, that would be controlled by parameter \(k\), i.e. carrying capacity. Also, if there is no wind or no surface inclination, the diffusivity parameter \(D\) is scalar. On the contrary, if the ground has some inclination or wind is present, the fire will have a tendency to go up the hill or follow the direction of the wind, that would be accounted for by tensorial representation of diffusivity. If the grass is of uniform height, \(D\) is equal everywhere, i.e. homogenous. If, for example, the height of the grass varies from one place to another, diffusivity and rate factor is heterogeneous, i.e. \(D=D(\mathbf{x})\) and \(r=r(\mathbf{x})\).
In this example, to keep the problem as simple as possible, we implement a homogenous case, with isotropic diffusivity. Moreover, we assume that fire is initiated at two places, as shown in Figure 1 below.

Figure 1: Two yellow spots are placed where the fire is initiated. On boundary, Dirichlet boundary condition u = 0 is applied.
- Note
- The estimated speed of the advancing wave can be used further to choose the duration of analysis and length of the time step.
Running code
The code can run in parallel, so before starting the analysis, we have to do mesh partitioning, such that, from very beginning, each processor stores in the memory only one part of the mesh. In order to partition mesh, execute the script in build directory in directory basic_finite_elements/reaction_diffusion_equation
NBPROC=6 && ../../tools/mofem_part \
-my_file mesh.cub -output_file mesh.h5m -my_nparts $NBPROC -dim 2 -adj_dim 1
where variable NBPROC represents the number of processors. The mesh file mesh.cub is the initial mesh which can be generated by a preprocessor, for example Cubit in this case. The partitioned mesh is saved to file mesh.h5m. Having that mesh at hand, we can solve the problem by running the command line below
time mpirun -np $NBPROC ./reaction_diffusion_equation 2>&1 | tee log
with the necessary parameters to run calculations found in the file param_file.petsc which is stored in the working directory
The key parameters are
- -ts_max_time: time duration
- -ts_dt: time step size
- -ts_arkimex_type: ARKIMEX time integration type
- -ts_adapt_type: time step adaptation (if the stiff part is not updated, it has to be set to node)
- -snes_lag_jacobian: determines how often jacobian (stiff part) is updated. If set to -2 jacobian is calculated only once at the beginning of the analysis

Figure 2: Solution of the problem.
Discretisation
Semi-discrete form of the equation
To solve the equation, we apply standard Galerkin method, used in finite element approximation, i.e. multiplying both sides by a test function and integrating by parts to reduce the demand for the regularity of the tested and testing functions, we get
\[ \int_\Omega v \frac{\partial u}{\partial t} \textrm{d}\Omega + \int_\Omega \nabla v \cdot D \nabla u \textrm{d}\Omega = \int_\Omega v r u \left(1-\frac{u}{k}\right) \textrm{d}\Omega \]
where \(\Omega\) is the solution Domain. To have a unique solution, we have to a priori enforce essential boundary conditions, such that the test functions \(v\) and tested function \(u\) disappear on the boundary \(\partial\Omega\). Also, the approximation and tested functions are in Hilbert space \(H^1_0(\Omega)\), such that the integral of the first derivative and function value over the domain is bounded. That will make the solution for our weak equation stable and equal to the solution of the strong equation, if smooth enough initial and boundary conditions are provided. Moreover, the solution to the problem can be approximated by a finite-dimensional and complete set of the piecewise mesh conforming polynomials, which are dense in \(H^1(\Omega)\), thus we will have convergence of the approximate solution to the exact solution with mesh refinement or increasing polynomial approximation order. The approximation of test and tested functions is given as follows
\[ v^h = \pmb\Phi \overline{\mathbf{v}}^\textrm{T} \quad\textrm{and}\quad u^h = \pmb\Phi \overline{\mathbf{u}}^\textrm{T} \]
where \(\pmb\Phi\) is the vector of hierarchical base functions, and \(\overline{\mathbf{v}}\), \(\overline{\mathbf{u}}\) are vectors of coefficients at degrees of freedom. Utilising finite element approximation functions we finally get semi-discrete form of the Fisher's equation
\[ \mathbf{M} \frac{\partial \overline{\mathbf{u}}}{\partial t} + \mathbf{K} \overline{\mathbf{u}} = \mathbf{G} \]
where
\[ \mathbf{M} := \int_\Omega \pmb\Phi^\textrm{T} \pmb\Phi\, \textrm{d}\Omega,\quad \mathbf{K} := \int_\Omega \nabla \pmb\Phi^\textrm{T} \nabla \pmb\Phi \, \textrm{d}\Omega\quad\textrm{and}\quad \mathbf{G} := \int_\Omega \pmb\Phi^\textrm{T} \left\{ r u^h \left(1-\frac{u^h}{k}\right) \right\} \, \textrm{d}\Omega \]
where \(\mathbf{M}\) is so called mass matrix, \(\mathbf{K}\) stiffness matrix and \(\mathbf{G}\) is source vector.
Time discretisation
In this section, we fully rely on time stepping algorithms briefly described in PETSc documentation in section 6. Moreover, we focus attention on IMEX method, i.e. implicit-explicit time integration. The IMEX method is particularly useful whereby two time scales are separated and present in the solution, i.e. one fast scale, associated with stiff part of a differential equation, and slow scale usually associated with the strongly nonlinear part of the equation. In our particular case, stiff part of the equation is assisted with the diffusion process, and slow is associated with the reaction part of the equation. Focusing attention on our example of fire propagation, in the plane of dry grass, stiff part controls the speed of advancing fire, and slow part is related to the length of the burning process itself, which takes a bit longer time. Using formalism presented in PETSc documentation, we have
\[ \mathbf{F} \left( t,\overline{\mathbf{u}^n}, \dot{\overline{\mathbf{u}^n}} \right) = \mathbf{G} \left( t,\overline{\mathbf{u}^n} \right) \]
where
\[ \left. \frac{\textrm{d}\mathbf{F}}{\textrm{d}\overline{\mathbf{u}}} \right|_{\overline{\mathbf{u}^n}} = \sigma \mathbf{F}_{\dot{\overline{\mathbf{u}^n}}} \left( t,\overline{\mathbf{u}^n}, \dot{\overline{\mathbf{u}^n}} \right) + \mathbf{F}_{\overline{\mathbf{u}^n}} \left( t,\overline{\mathbf{u}^n}, \dot{\overline{\mathbf{u}^n}} \right) = \sigma \mathbf{M} + \mathbf{K} \]
where
\[ \sigma = \left. \frac{\partial \dot{u}}{\partial u} \right|_{u^n} \]
is the parameter provided by the algorithm of time integration, implemented in PETSc. The key advantage of the presented algorithm is that implementation of the equation is independent on time integration algorithm, and user can freely and quickly change time integration method without need of changing a line of the code. The change of time integration scheme is accounted by \(\sigma\).
Implementation
Total control of the solution process including calling functions to calculate matrices and vectors in the right order is handled by PETSc time solver (TS). TS calls MoFEM methods iterating over finite element entities, which are provided by Discrete Manager (DM). MoFEM is responsible for managing degrees of freedom, finite elements, and iterating over entities on the mesh. MOAB is the mesh database where all data is stored on mesh tags at any point of the analysis.
MoFEM and MOAB databases provide low-level functions, however in this case flexibility of MoFEM::Simple interface is adequate. MoFEM::Simple interface creates approximation fields and finite elements on the whole mesh, and it creates problem data structures accessed by DM. DM is a bridge between PETSc and MoFEM data structures and functions, in this particular case TS.
The programmer responsibility is to initialise data structures, methods and provide users operators, called by finite elements, to evaluate matrices and vectors when called by time solver (TS). The relation between TS functions, DM in MoFEM and finite elements are shown in Figure 3.
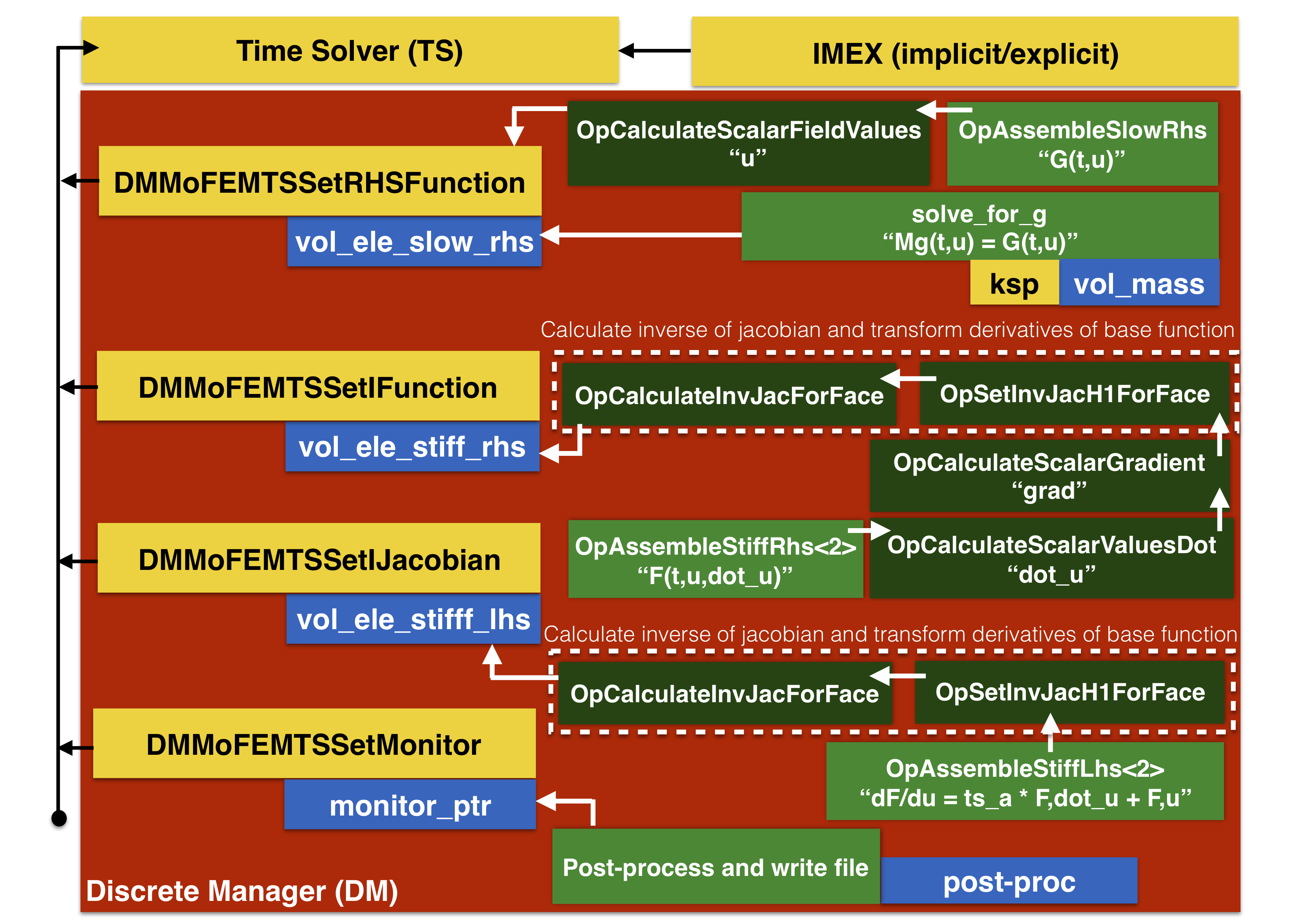
Figure 3: Finite elements and operators. Yellow colour indicates functions related to TS. Red colour indicates functions managed by DM. Blue colour indicates finite element instances. Green colour indicates user data operators, where dark green represents standard user data operators, and light green represents user data operators implemented for this tutorial
Implementation of the problem is for PDE in 2D, however, with minimal effort changing the type of element, it can be extended to 3D. Moreover is independent on time integration method, exploiting how PETSc time solver is implemented. width=800p
Setup problem
MoFEM always has to start with initialisation and the main function has the followwing format
int main(
int argc,
char *argv[]) {
const char param_file[] = "param_file.petsc";
try {
}
return 0;
}
It is worth noting that almost all MoFEM, PETSc and MOAB functions should be checked by CHKERR which is essential for safe code development and error detection.
In this tutorial, the initialisation of the database contains following steps
- Main code starts with creating MOAB database and MoFEM database instances and intefaces to each of them
- Registration of MoFEM Discrete Manager in PETSc
DMType dm_name = "DMMOFEM";
- Loading mesh, adding fields and setting-up DM manager
Simple *simple_interface;
CHKERR simple_interface->getOptions();
CHKERR simple_interface->loadFile();
1);
CHKERR simple_interface->setUp();
Note that here we add only one field u, in \(H^1(\Omega)\) space, approximation base is constructed following AINSWORTH_LEGENDRE_BASE recipe, and field is scalar, i.e. number of coefficients for base function is 1. Simple interface presumes that the field is spanned over the whole domain, and integration in domain will be performed over the highest dimension entities on the mesh, in this particular example, all triangles. The finite element name is accessed through std::string fe_name = simple_interface->getDomainFEName();
- Getting access to the database from this point can be done exclusively through DM Note that MoFEM::SmartPetscObj wraps PETSc object so that they can be used as a regular PETSc object but the user is relieved from the need of calling the destructor for it. Having access to DM, one can push finite element instances which can be used by TS to calculate matrices and vectors at subsequent time steps.
Telling TS which elements should be used
In Figure 3, yellows are PETSc functions and those on red background are part of DM, interfacing TS with MoFEM. In this tutorial TS is set to use IMEX (implicit/explicit) method, see details in section 6. Methods calculating vector and matrices needed by TS solver to proceed set by DM functions, are as follows
- MoFEM::DMMoFEMTSSetRHSFunction to calculate \(\mathbf{G}\)
- MoFEM::DMMoFEMTSSetIFunction to calculate \(\mathbf{F}\)
- MoFEM::DMMoFEMTSSetIJacobian to calculate \(\left. \frac{\textrm{d}\mathbf{F}}{\textrm{d}\overline{\mathbf{u}}} \right|_{\overline{\mathbf{u}^n}}\)
- MoFEM::DMMoFEMTSSetMonitor to set monitor run at the end of each load step
Those functions provide sequences of finite elements (or just one element for each term in this particular case) to calculate entries of vectors and matrices at specific time steps.
Blue boxes mark finite elements in Figure 3 are created by the following code
boost::shared_ptr<Ele> vol_ele_slow_rhs(
new Ele(m_field));
boost::shared_ptr<Ele> vol_ele_stiff_rhs(
new Ele(m_field));
boost::shared_ptr<Ele> vol_ele_stiff_lhs(
new Ele(m_field));
where integration rule, controlling number of integration points on each element are set by
auto vol_rule = [](
int,
int,
int p) ->
int {
return 2 * p; };
vol_ele_slow_rhs->getRuleHook = vol_rule;
vol_ele_stiff_rhs->getRuleHook = vol_rule;
vol_ele_stiff_lhs->getRuleHook = vol_rule;
The integration rule depends on the type of operator evaluated on the element, in our case, we evaluate mass matrices, thus we need to calculate integrals exactly with polynomial order \(2p\).
Note that finite element instances implementation is generic. Elements do problem specific calculations by providing to them user data operators which will be described in the following sections. Three elements vol_ele_slow_rhs, vol_ele_stiff_rhs and vol_ele_stiff_lhs are provided to Discrete Manager (DM) to calculate slow and stiff vectors and Jacobian matrix. Those three elements are instances of the class MoFEM::FaceElementForcesAndSourcesCore. Once elements are created, we can add them to the TS manager through the DM interface
vol_ele_stiff_lhs, null, null);
vol_ele_stiff_rhs, null, null);
vol_ele_slow_rhs, null, null);
- Note
- In case of 3D problem, user has to switch to MoFEM::VolumeElementForcesAndSourcesCore to integrate over volume entities. Note that all users operators implemented in the example are templates, where the template variable is the dimension of the element. That makes implementation dimension independent.
Telling finite elements which operators should be used
The problem specific matrices and vectors are implemented in namespace ReactionDiffusionEquation, by users data operators ReactionDiffusionEquation::OpEle. In this tutorial, following operators are implemented
- ReactionDiffusionEquation::OpAssembleMass used to calculate mass matrix \(\mathbf{M}\)
- ReactionDiffusionEquation::OpAssembleSlowRhs used to calculate the slow right-hand side vector \(\mathbf{G}\)
- ReactionDiffusionEquation::OpAssembleStiffRhs used to calculate the stiff vector \(\mathbf{F}\)
- ReactionDiffusionEquation::OpAssembleStiffLhs used to calculate the stiff matrix \(\frac{\textrm{d}\mathbf{F}}{\textrm{d} \overline{\mathbf{u}^n}}\)
- ReactionDiffusionEquation::Monitor used to post-process results at the end of each time step
Implementation of each operator follows a similar pattern,
- The class is inherited from ReactionDiffusionEquation::OpEle
- Two types of operators are implemented ReactionDiffusionEquation::OpEle::OPROW to calculate vectors, and ReactionDiffusionEquation::OpEle::OPROWCOL to calculate matrices.
- Implementation of user operator overload doWork member function
- In each doWork method, user iterates over integration points, and then over base functions. In case of a matrix, over base functions on rows and columns.
- Once local element vector is assembled, doWork function is finalised with assembling to global vector or global matrix.
- Note
- More detail description on how to implement user data operator can be found in other tutorials, for example, COR-3: Implementing operators for the Poisson equation.
Common data
The data between the operator and finite elements are passed through ReactionDiffusionEquation::CommonData
which is dynamically allocated and kept by shared pointer
boost::shared_ptr<CommonData> data(
new CommonData());
in addition some other operators need direct access to data, it can be safely done by so called aliased shared pointers (see here)
auto val_ptr = boost::shared_ptr<VectorDouble>(data, &data->val);
auto dot_val_ptr = boost::shared_ptr<VectorDouble>(data, &data->dot_val);
auto grad_ptr = boost::shared_ptr<MatrixDouble>(data, &data->grad);
Pushing operators to finite element
Each of those user data operators are added to finite element, for example to vol_ele_stiff_rhs we add operators as following
auto det_ptr = boost::make_shared<VectorDouble>();
auto jac_ptr = boost::make_shared<MatrixDouble>();
auto inv_jac_ptr = boost::make_shared<MatrixDouble>();
vol_ele_stiff_rhs->getOpPtrVector().push_back(new OpCalculateHOJac<2>(jac_ptr));
vol_ele_stiff_rhs->getOpPtrVector().push_back(new OpInvertMatrix<2>(jac_ptr, det_ptr, inv_jac_ptr));
vol_ele_stiff_rhs->getOpPtrVector().push_back(new
vol_ele_stiff_rhs->getOpPtrVector().push_back(new
vol_ele_stiff_rhs->getOpPtrVector().push_back(new
vol_ele_stiff_rhs->getOpPtrVector().push_back(new
where MoFEM::OpCalculateJacForFace, and MoFEM::OpSetHOInvJacToScalarBases<2> are standard operators to calculate element inverse of jacobian, and pull derivatives of base functions to element reference configuration
\[ \frac{\partial \pmb\Phi}{\partial \mathbf{x}} = \frac{\partial \pmb\Phi}{\partial \pmb\xi}\mathbf{J}^{-\textrm{T}} \quad\textrm{where}\quad \mathbf{J} = \frac{\partial \mathbf{x}}{\partial \pmb\xi},\; \mathbf{x} = \pmb\Phi(\pmb \xi) \overline{\mathbf{x}} \]
where \(\pmb \xi\) are coordinates in local element configuration, \(\overline{\mathbf{x}}\) are nodal positions or higher order coefficients in edges and faces if necessary to describe higher order geometry. Operators MoFEM::OpCalculateScalarFieldGradient and MoFEM::OpCalculateScalarFieldGradient are standard operators and are used to calculate field values, and gradients of field values at integration points, respectively. All operators in Figure 3 marked by dark green color are standard operators and are implemented in basic user modules.
Problem with IMAX method in TS
The implementation of IMAX method in TS solver requires the user to provide
\[ \mathbf{g}(t,\overline{\mathbf{u}}) = \mathbf{M}^{-1}\mathbf{G}(t,\overline{\mathbf{u}}) \]
whereas user data operators provide vector \(\mathbf{G}(t,\overline{\mathbf{u}})\). This issue can be resolved by exploiting finite element functionality. Each finite element class is derived from MoFEM::BasicMethod
struct BasicMethod : public KspMethod, SnesMethod, TSMethod {
if(preProcessHook)
}
if(preProcessHook)
}
};
Every element is run in three stages
- preProcess() is executed before the code iterates over all given entity finite elements on the mesh
- operator() is executed for each entity of finite element on the mesh
- postProcess() is executed after the code iterates over all given entity finite elements on the mesh
If user provides hook to postProcess stage, after vector \(\mathbf{G}(t,\overline{\mathbf{u}})\) is calculated, can solve on place for \(\mathbf{g}(t,\overline{\mathbf{u}})\). This is done by following lambda function
auto solve_for_g = [&]() {
if (*(vol_ele_slow_rhs->vecAssembleSwitch)) {
CHKERR VecGhostUpdateBegin(vol_ele_slow_rhs->ts_F, ADD_VALUES, SCATTER_REVERSE);
CHKERR VecGhostUpdateEnd(vol_ele_slow_rhs->ts_F, ADD_VALUES, SCATTER_REVERSE);
CHKERR VecAssemblyBegin(vol_ele_slow_rhs->ts_F);
CHKERR VecAssemblyEnd(vol_ele_slow_rhs->ts_F);
*vol_ele_slow_rhs->vecAssembleSwitch = false;
}
CHKERR KSPSolve(data->ksp, vol_ele_slow_rhs->ts_F, vol_ele_slow_rhs->ts_F);
};
The lambda function is set as a hook to the slow finite element, i.e. vol_ele_slow_rhs as follows
vol_ele_slow_rhs->postProcessHook =
solve_for_g;
Note, that is also indicated on Figure 3. In solve_for_g the KSP (linear) solver is used to solve linear equation
\[ \mathbf{M}\mathbf{g}(t,\overline{\mathbf{u}}) = \mathbf{G}(t,\overline{\mathbf{u}}) \]
where mass matrix \(\mathbf{M}\) is calculated as follows
CHKERR MatZeroEntries(data->M);
boost::shared_ptr<Ele> vol_mass_ele(
new Ele(m_field));
vol_mass_ele->getOpPtrVector().push_back(new
CHKERR MatAssemblyBegin(data->M, MAT_FINAL_ASSEMBLY);
CHKERR MatAssemblyEnd(data->M, MAT_FINAL_ASSEMBLY);
with the use on the fly created finite element vol_mass_ele with pushed one operator ReactionDiffusionEquation::OpAssembleMass. The linear KSP solver is created and set up as follows
CHKERR KSPSetOperators(data->ksp, data->M, data->M);
CHKERR KSPSetFromOptions(data->ksp);
CHKERR KSPSetUp(data->ksp);
Initial and boundary conditions
Initial conditions
To set initial conditions, we use MoFEM::MeshsetsManager to get entities on the blockset, which are set by mesh generators, for example, Cubit, Salome or gMEsh. We assume that entities on which we set boundary conditions are set on a subset of entities, which are listed in BLOCKSET 1 in the following code
if (!inner_surface.empty()) {
Range inner_surface_verts;
CHKERR moab.get_connectivity(inner_surface, inner_surface_verts,
false);
u0, MBVERTEX, inner_surface_verts,
"u");
}
}
- We check if BLOCKSET 1 exist. Since the problem is solved in parallel, each the processor keeps only part of the mesh, BLOCKSET 1 exists only on some processors with the right set of the entities
- If the blockset exists, we ask MoFEM::MeshsetsManager to give entities dimension 2, i.e. faces, i.e. triangles in the blockset
- We get all the vertices on faces, and using MoFEM::FieldBlas interface we set values to the nodes on vertices. The value which is set is constant \(u_0\).
Dirichlet boundary conditions
To keep initial assumption, given in the beginning paragraphs about fire propagation, that around the plain of dry grass we have a closed trench filled with water, we will apply homogenous Dirichlet boundary conditions on the boundary of the domain. To do that we follow the code
ParallelComm *pcomm = ParallelComm::get_pcomm(&moab,
MYPCOMM_INDEX);
CHKERR pcomm->filter_pstatus(edges, PSTATUS_SHARED | PSTATUS_MULTISHARED,
PSTATUS_NOT, -1, &edges_part);
CHKERR moab.get_connectivity(edges_part, edges_verts,
false);
simple_interface->getProblemName(), "u",
unite(edges_verts, edges_part));
- Take all triangles on the mesh
- Using Skinner implemented in MOAB, we take skin from the mesh. Consequently we have all edges bounding part of the mesh.
- Since we work on the parallel partitioned mesh, not all edges are on true domain boundary. In order to filter out true boundary we use moab::ParallelComm::filter_pstatus which is provided with MOAB interface. Using moab::ParallelComm::filter_pstatus, we filter out all entities that are not shared with any other processors. Finally, we obtain entities on physical domain boundary.
- In order to enforce homogenous essential boundary conditions in the finite element method, the simplest way is to remove degrees of freedom (DOFs) from the problem. That is done by MoFEM::ProblemsManager interface using MoFEM::ProblemsManager::removeDofsOnEntities function. MoFEM::ProblemsManager is a MoFEM interface to manage DOFs and finite elements on the problem.
The plain program.
The plain program is located in basic_finite_elements/reaction_diffusion_equation/reaction_diffusion.cpp
static char help[] =
"...\n\n";
};
struct OpAssembleMass :
OpEle {
OpAssembleMass(boost::shared_ptr<CommonData> &data)
:
OpEle(
"u",
"u",
OpEle::OPROWCOL), commonData(data) {
sYmm = true;
}
MoFEMErrorCode doWork(
int row_side,
int col_side, EntityType row_type,
EntityType col_type,
EntData &row_data,
const int nb_row_dofs = row_data.
getIndices().size();
const int nb_col_dofs = col_data.
getIndices().size();
if (nb_row_dofs && nb_col_dofs) {
const int nb_integration_pts = getGaussPts().size2();
mat.resize(nb_row_dofs, nb_col_dofs, false);
mat.clear();
auto t_w = getFTensor0IntegrationWeight();
const double vol = getMeasure();
for (int gg = 0; gg != nb_integration_pts; ++gg) {
const double a = t_w * vol;
for (int rr = 0; rr != nb_row_dofs; ++rr) {
for (int cc = 0; cc != nb_col_dofs; ++cc) {
mat(rr, cc) +=
a * t_row_base * t_col_base;
++t_col_base;
}
++t_row_base;
}
++t_w;
}
ADD_VALUES);
if (row_side != col_side || row_type != col_type) {
transMat.resize(nb_col_dofs, nb_row_dofs, false);
noalias(transMat) = trans(mat);
ADD_VALUES);
}
}
}
private:
boost::shared_ptr<CommonData> commonData;
};
struct OpAssembleSlowRhs :
OpEle {
OpAssembleSlowRhs(boost::shared_ptr<CommonData> &data)
if (nb_dofs) {
vecF.resize(nb_dofs, false);
vecF.clear();
const int nb_integration_pts = getGaussPts().size2();
auto t_w = getFTensor0IntegrationWeight();
const double vol = getMeasure();
for (int gg = 0; gg != nb_integration_pts; ++gg) {
const double a = vol * t_w;
const double f =
a *
r * t_val * (1 - t_val /
k);
for (int rr = 0; rr != nb_dofs; ++rr) {
const double b =
f * t_base;
vecF[rr] += b;
++t_base;
}
++t_val;
++t_w;
}
CHKERR VecSetOption(getFEMethod()->ts_F, VEC_IGNORE_NEGATIVE_INDICES,
PETSC_TRUE);
ADD_VALUES);
}
}
private:
boost::shared_ptr<CommonData> commonData;
};
template <
int DIM>
struct OpAssembleStiffRhs :
OpEle {
OpAssembleStiffRhs(boost::shared_ptr<CommonData> &data)
if (nb_dofs) {
vecF.resize(nb_dofs, false);
vecF.clear();
const int nb_integration_pts = getGaussPts().size2();
auto t_grad = getFTensor1FromMat<DIM>(commonData->grad);
auto t_w = getFTensor0IntegrationWeight();
const double vol = getMeasure();
for (int gg = 0; gg != nb_integration_pts; ++gg) {
const double a = vol * t_w;
for (int rr = 0; rr != nb_dofs; ++rr) {
vecF[rr] +=
a * (t_base * t_dot_val +
D * t_diff_base(
i) * t_grad(
i));
++t_diff_base;
++t_base;
}
++t_dot_val;
++t_grad;
++t_w;
}
CHKERR VecSetOption(getFEMethod()->ts_F, VEC_IGNORE_NEGATIVE_INDICES,
PETSC_TRUE);
ADD_VALUES);
}
}
private:
boost::shared_ptr<CommonData> commonData;
};
template <
int DIM>
struct OpAssembleStiffLhs :
OpEle {
OpAssembleStiffLhs(boost::shared_ptr<CommonData> &data)
:
OpEle(
"u",
"u",
OpEle::OPROWCOL), commonData(data) {
sYmm = true;
}
MoFEMErrorCode doWork(
int row_side,
int col_side, EntityType row_type,
EntityType col_type,
EntData &row_data,
const int nb_row_dofs = row_data.
getIndices().size();
const int nb_col_dofs = col_data.
getIndices().size();
if (nb_row_dofs && nb_col_dofs) {
mat.resize(nb_row_dofs, nb_col_dofs, false);
mat.clear();
const int nb_integration_pts = getGaussPts().size2();
auto t_w = getFTensor0IntegrationWeight();
const double ts_a = getFEMethod()->ts_a;
const double vol = getMeasure();
for (int gg = 0; gg != nb_integration_pts; ++gg) {
const double a = vol * t_w;
for (int rr = 0; rr != nb_row_dofs; ++rr) {
for (int cc = 0; cc != nb_col_dofs; ++cc) {
mat(rr, cc) +=
a * (t_row_base * t_col_base * ts_a +
D * t_row_diff_base(
i) * t_col_diff_base(
i));
++t_col_base;
++t_col_diff_base;
}
++t_row_base;
++t_row_diff_base;
}
++t_w;
}
ADD_VALUES);
if (row_side != col_side || row_type != col_type) {
transMat.resize(nb_col_dofs, nb_row_dofs, false);
noalias(transMat) = trans(mat);
&transMat(0, 0), ADD_VALUES);
}
}
}
private:
boost::shared_ptr<CommonData> commonData;
};
: dM(dm), postProc(post_proc){};
"out_level_" + boost::lexical_cast<std::string>(ts_step) + ".h5m");
}
}
private:
boost::shared_ptr<PostProcEle> postProc;
};
};
int main(
int argc,
char *argv[]) {
const char param_file[] = "param_file.petsc";
try {
DMType dm_name = "DMMOFEM";
1);
boost::shared_ptr<CommonData> data(
new CommonData());
auto val_ptr = boost::shared_ptr<VectorDouble>(data, &data->val);
auto dot_val_ptr = boost::shared_ptr<VectorDouble>(data, &data->dot_val);
auto grad_ptr = boost::shared_ptr<MatrixDouble>(data, &data->grad);
boost::shared_ptr<Ele> vol_ele_slow_rhs(
new Ele(m_field));
boost::shared_ptr<Ele> vol_ele_stiff_rhs(
new Ele(m_field));
boost::shared_ptr<Ele> vol_ele_stiff_lhs(
new Ele(m_field));
vol_ele_slow_rhs->getOpPtrVector().push_back(
vol_ele_slow_rhs->getOpPtrVector().push_back(new OpAssembleSlowRhs(data));
auto solve_for_g = [&]() {
if (*(vol_ele_slow_rhs->vecAssembleSwitch)) {
CHKERR VecGhostUpdateBegin(vol_ele_slow_rhs->ts_F, ADD_VALUES,
SCATTER_REVERSE);
CHKERR VecGhostUpdateEnd(vol_ele_slow_rhs->ts_F, ADD_VALUES,
SCATTER_REVERSE);
CHKERR VecAssemblyBegin(vol_ele_slow_rhs->ts_F);
CHKERR VecAssemblyEnd(vol_ele_slow_rhs->ts_F);
*vol_ele_slow_rhs->vecAssembleSwitch = false;
}
CHKERR KSPSolve(data->ksp, vol_ele_slow_rhs->ts_F,
vol_ele_slow_rhs->ts_F);
};
vol_ele_slow_rhs->postProcessHook = solve_for_g;
auto det_ptr = boost::make_shared<VectorDouble>();
auto jac_ptr = boost::make_shared<MatrixDouble>();
auto inv_jac_ptr = boost::make_shared<MatrixDouble>();
vol_ele_stiff_rhs->getOpPtrVector().push_back(
vol_ele_stiff_rhs->getOpPtrVector().push_back(
vol_ele_stiff_rhs->getOpPtrVector().push_back(
vol_ele_stiff_rhs->getOpPtrVector().push_back(
vol_ele_stiff_rhs->getOpPtrVector().push_back(
vol_ele_stiff_rhs->getOpPtrVector().push_back(
new OpAssembleStiffRhs<2>(data));
vol_ele_stiff_lhs->getOpPtrVector().push_back(
vol_ele_stiff_lhs->getOpPtrVector().push_back(
vol_ele_stiff_lhs->getOpPtrVector().push_back(
vol_ele_stiff_lhs->getOpPtrVector().push_back(
new OpAssembleStiffLhs<2>(data));
auto vol_rule = [](
int,
int,
int p) ->
int {
return 2 * p; };
vol_ele_slow_rhs->getRuleHook = vol_rule;
vol_ele_stiff_rhs->getRuleHook = vol_rule;
vol_ele_stiff_lhs->getRuleHook = vol_rule;
auto post_proc = boost::make_shared<PostProcEle>(m_field);
boost::shared_ptr<ForcesAndSourcesCore> null;
auto u_ptr = boost::make_shared<VectorDouble>();
post_proc->getOpPtrVector().push_back(
post_proc->getOpPtrVector().push_back(
post_proc->getPostProcMesh(), post_proc->getMapGaussPts(),
{{"u", u_ptr}},
{},
{},
{}
)
);
auto dm = simple_interface->
getDM();
if (!inner_surface.empty()) {
Range inner_surface_verts;
CHKERR moab.get_connectivity(inner_surface, inner_surface_verts,
false);
u0, MBVERTEX, inner_surface_verts,
"u");
}
}
ParallelComm *pcomm = ParallelComm::get_pcomm(&moab,
MYPCOMM_INDEX);
CHKERR pcomm->filter_pstatus(edges, PSTATUS_SHARED | PSTATUS_MULTISHARED,
PSTATUS_NOT, -1, &edges_part);
CHKERR moab.get_connectivity(edges_part, edges_verts,
false);
unite(edges_verts, edges_part));
CHKERR MatZeroEntries(data->M);
boost::shared_ptr<Ele> vol_mass_ele(
new Ele(m_field));
vol_mass_ele->getOpPtrVector().push_back(new OpAssembleMass(data));
vol_mass_ele);
CHKERR MatAssemblyBegin(data->M, MAT_FINAL_ASSEMBLY);
CHKERR MatAssemblyEnd(data->M, MAT_FINAL_ASSEMBLY);
CHKERR KSPSetOperators(data->ksp, data->M, data->M);
CHKERR KSPSetFromOptions(data->ksp);
CHKERR TSSetType(ts, TSARKIMEX);
CHKERR TSARKIMEXSetType(ts, TSARKIMEXA2);
vol_ele_stiff_lhs, null, null);
vol_ele_stiff_rhs, null, null);
vol_ele_slow_rhs, null, null);
boost::shared_ptr<Monitor> monitor_ptr(
new Monitor(dm, post_proc));
monitor_ptr, null, null);
double ftime = 1;
CHKERR TSSetDuration(ts, PETSC_DEFAULT, ftime);
}
return 0;
}





