 |
v0.14.0 |
 |
v0.14.0 |
The solution of the wave propagation problem in the frequency domain by means of the Finite Element Method is presented in this tutorial. The wave equation is:
\[ \begin{align} \label{eq:one} \dfrac{{\partial}^2 P({\mathbf{x}}, t)}{\partial t^2} - c^2 {\nabla}^2 P({\mathbf{x}}, t) = 0 \quad \text{in } \Omega \end{align} \]
that is true in the whole domain of the problem under consideration that is the grey area in Figure 1. Variable \(c\) is the wave speed assumed to be constant and \( P({\mathbf{x}}, t) \) is the spatially and temporally varying pressure, with spatial position vector \({\mathbf{x}} \in \mathbb{R}^2\) and time \(t \in \mathbb{R}^{+}\).
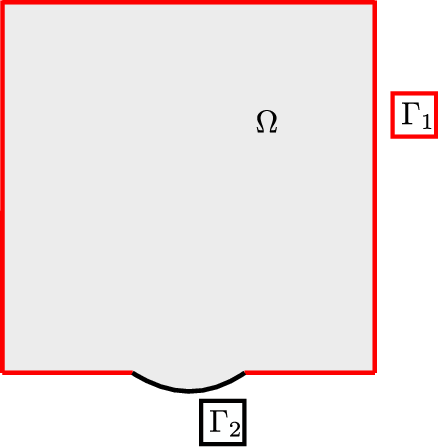
Quasi-absorbing boundary conditions are assumed for part of the boundary of the domain \(\Gamma_1\), as presented with red line in Figure 1, defined as
\[ \begin{align} \label{eq:two} \dfrac{\partial P({\mathbf{x}}, t)}{\partial t} + c\left({\mathbf{N}} \cdot \nabla P ({\mathbf{x}}, t) \right) = 0 \quad \text{on } \Gamma_1 \end{align} \]
where \(\mathbf{N}\) is the unit normal vector on the quasi absorbing boundary, \(\Gamma_1\).
A source of constant frequency, \(\omega\), and amplitude is assumed to be located on a different part of the boundary of the domain \(\Gamma_2\):
\[ \begin{align} \label{eq:three} P({\mathbf{x}}, t) = {\rm {cos}}(\omega t) \quad \text{on } \Gamma_2 \end{align} \]
where \(\Gamma_1\) is presented with black line in Figure 1,
Since we focus attention on a single frequency, we solve the problem in the frequency domain, reducing problem complexity. Assuming that the solution can admit variable separation:
\[ \begin{align} \label{eq:four} P({\mathbf{x}}, t) = {\rm Re}({p(\mathbf{x}) e^{-i \omega t} }) \end{align} \]
where now the spatially varying pressure amplitude, \(p(\mathbf{x})\), a complex value:
\[ \begin{align} \label{eq:five} p({\mathbf{x}}) = p^{\rm{Re}} + i p^{\rm{Im}} \end{align} \]
By introducing the wave number \(k = \omega / c \) and substituting \eqref{eq:four} and \eqref{eq:five} in \eqref{eq:one} to \eqref{eq:three} we arrive to the Helmholtz problem:
\[ \begin{equation} \begin{aligned} \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} k^2 p^{\rm {Re}} + {\nabla}^2 p^{\rm {Re}} = 0 \\ k^2 p^{\rm {Im}} + {\nabla}^2 p^{\rm {Im}} = 0 \\ \end{rcases} {\text {in }} \Omega,\quad \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} \mathbf{N} \cdot \nabla p^{\rm {Re}} + k p^{\rm {Im}} = 0 \\ \mathbf{N} \cdot \nabla p^{\rm {Im}} - k p^{\rm {Re}} = 0 \\ \end{rcases} {\text {on }} \Gamma_1,\quad \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} p^{\rm {Re}} = 1 \\ p^{\rm {Im}} = 0 \\ \end{rcases} {\text {on }} \Gamma_2 \label{eq:six} \end{aligned} \end{equation} \]
It can be observed that the imaginary number \(i\) has disappeared since one can operate on the real and imaginary parts of the equation separately to fullfil an equation that is equal to zero. Therefore, the original problem of a single field, \( P({\mathbf{x}}, t) \), into a two field problem where one field is \(p^{\rm {Re}}\) and the second one \(p^{\rm {Re}}\).
In this section the weak formulation is going to be presented and then extended to the equivalent discrete formulation. The weak formulation reads as this:
Find \( p^{\rm {Re}}\) and \(p^{\rm {Re}} \in H^1(\Omega) \) such that:
\[ \begin{equation} \begin{aligned} \label{eq:seven} \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} k^2 {\int_{\Omega}} p^{\rm {Re}}\delta p^{\rm {Re}} {\rm d} {\Omega}+ {\int_{\Omega}}{\nabla}^2 p^{\rm {Re}} \delta p^{\rm {Re}}{\rm d} {\Omega} = 0 \\ k^2 {\int_{\Omega}} p^{\rm {Im}} \delta p^{\rm {Im}} {\rm d} {\Omega}+ {\int_{\Omega}}{\nabla}^2 p^{\rm {Im}}\delta p^{\rm {Im}}{\rm d} {\Omega} = 0 \\ \end{rcases} {\text {in }} \Omega,\quad \forall \delta p^{\rm {Re}}, \delta p^{\rm {Im}} \in H^1_0(\Omega)\\ \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} {\int_{\Gamma_1}}\mathbf{N} \cdot \nabla p^{\rm {Re}} \delta p^{\rm {Re}} {\rm d} {\Gamma_1}+ {\int_{\Gamma_1}}k p^{\rm {Im}} \delta p^{\rm {Re}} {\rm d} {\Gamma_1}= 0 \\ {\int_{\Gamma_1}}\mathbf{N} \cdot \nabla p^{\rm {Im}} \delta p^{\rm {Im}} {\rm d} {\Gamma_1} - {\int_{\Gamma_1}}k p^{\rm {Re}} \delta p^{\rm {Im}} {\rm d} {\Gamma_1}= 0 \\ \end{rcases} {\text {on }} \Gamma_1,\quad \forall \delta p^{\rm {Re}}, \delta p^{\rm {Im}} \in H^1_0(\Omega)\\ \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} {\int_{\Gamma_2}}p^{\rm {Re}} \delta p^{\rm {Re}} {\rm d} {\Gamma_2}= {\int_{\Gamma_2}}\delta p^{\rm {Re}} {\rm d} {\Gamma_2} \\ p^{\rm {Im}} = 0 \\ \end{rcases} {\text {on }} \Gamma_2,\quad \forall \delta p^{\rm {Re}}, \delta p^{\rm {Im}} \in H^1_0(\Omega) \end{aligned} \end{equation} \]
where \(\delta p^{\rm {Re}}\) and \(\delta p^{\rm {Im}}\) are the trial functions for the real and imaginary fields, respectively, and fulfil the identity, \( \delta p({\mathbf{x}}) = \delta p^{\rm {Re}} + i \delta p^{\rm {Im}}\).
By applying integration by parts for the laplacian term for the domain integral and substituting the
\[ \begin{equation} \begin{aligned} {p}^{\rm {Re}} \approx {p}^{h{\rm {Re}}} = \sum^{N-1}_{j = 0 } \phi_j {\bar {p}}^{\rm {Re}}_j, \quad {p}^{\rm {Im}} \approx {p}^{h{\rm {Im}}} = \sum^{N-1}_{j = 0 } \psi_j {\bar {p}}^{\rm {Im}}_j \label{eq:eight} \end{aligned} \end{equation} \]
the system of equations presented below are derived
\[ \begin{align} \label{eq:nine} \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} \sum^{N-1}_{j = 0 } (k^2 {\displaystyle{\int_{\Omega}}} \phi_i \phi_j {\rm{d}}\Omega - {\int_{\Omega}} \nabla \phi_i \nabla\phi_j {\rm{d}}\Omega) {\bar p}^{\rm{Re}}_j - k ({\displaystyle{\int_{\Gamma_1}}} \phi_i\psi_j {\rm{d}}\Gamma_1) {\bar p}^{\rm{Im}}_j = 0 \\ \sum^{N-1}_{j = 0 } (k^2 {\displaystyle{\int_{\Omega}}} \psi_i \psi_j {\rm{d}}\Omega - {\int_{\Omega}} \nabla \psi_i \nabla\psi_j {\rm{d}}\Omega) {\bar p}^{\rm{Im}}_j + k ({\displaystyle{\int_{\Gamma_1}}} \psi_i\phi_j {\rm{d}}\Gamma_1) {\bar p}^{\rm{Re}}_j = 0 \\ \end{rcases} \quad \forall i = 0, .... (N-1) \end{align} \]
after grouping the unknowns and their coefficients the matrix notation is obtained:
\[ \begin{align} \label{eq:ten} \left[ \begin{array}{c c} k^2 {\displaystyle{\int_{\Omega}}} \phi_i \phi_j {\rm{d}}\Omega - {\int_{\Omega}} \nabla \phi_i \nabla\phi_j {\rm{d}}\Omega & -k {\displaystyle{\int_{\Gamma_1}}} \phi_i\psi_j {\rm{d}}\Gamma_1 \\ \\ k{\displaystyle{\int_{\Gamma_1}}} \psi_i\phi_j {\rm{d}}\Gamma_1 & + k^2 \displaystyle{{\int_{\Omega}}} \psi_i \psi_j {\rm{d}}\Omega - \displaystyle{{\int_{\Omega}}} \nabla \psi_i \nabla\psi_j {\rm{d}}\Omega \end{array} \right] \left[ \begin{array}{c} {\bar {p}}^{\rm {Re}}_j \\[0.2cm] {\bar {p}}^{\rm {Im}}_j \end{array} \right] = \left[ \begin{array}{c} \mathbf 0 \\ \mathbf 0 \end{array} \right] \end{align} \]
And essential boundary conditions applied on \(\Gamma_2\) are after applying discretisation are
\[ \begin{align} \label{eq:eleven} \sum^{N-1}_{j = 0 } -\left({\displaystyle{\int_{\Gamma_2}}} \phi_i \phi_j {\rm{d}}\Gamma_2\right){\bar{p^{\rm{Re}}_j}} = -{\displaystyle{\int_{\Gamma_2}}} \phi_i {\rm{d}}\Gamma_2 \quad \forall i = 0,...(N-1) \end{align} \]
The focus of this section is on describing the procedure for solving two field problems in MoFEM using interface MoFEM::Simple, determining boundary conditions, using boundary and domain elements accessed through the interface and pushing form integrators to pipelines for solving the problem.
The focus of this section is on the points highlighted in the Notes in the beginning of the tutorial. The problem is run by execution of a series of functions when invoking the function Example::runProblem():
where Example::readMesh() executes the mesh reading procedure, then Example::setupProblem() involves adding the two unknown fields on the entities of the mesh and determine the base function space, base, field rank and base order
where the fields \(p^{\rm{Re}}\) and \(p^{\rm{Im}}\) are marked as P_REAL and P_IMAG, respectively. Furthermore, the space chosen is H1, the base is AINSWORTH_BERNSTEIN_BEZIER_BASE and dimension is 1 that corresponds to a scalar field. The field data is added both to Domain Element and Boundary Element from Simple Interface via invoking addDomainField and addBoundaryField, respectively. As it will be shown later, for a problem solved in \(\mathbb{R}^d\) where \( d \) is the problem dimension, Domain Elements perform operations on the mesh entities of the highest dimension ( \(\mathbb{R}^d\)) and Boundary Elements that perform operations on mesh entities of dimension \( d - 1\) that lie only on the boundary of the mesh, in this case \( \Gamma_1\) and \( \Gamma_2\).
Moreover, the base functions corresponding to \(p^{\rm{Re}}\) and to \(p^{\rm{Im}}\)
where the default value is set to be 6
and can be changed by determining the order of choice via the command line parameter -order. Finally, the fields are set up via simpleInterface->setUp().
Thereafter, the boundary entities are marked based on the input in Example::boundaryCondition() as shown in the snippet below
The present code is designated for 2D problems. Hence, all vertices and edges located on the \(\Gamma_2\) boundary, marked with BLOCK_SET with name "BC" in the input file, are added to the global variable Example::boundaryMarker that will be used in the assembly procedure. Furthermore, due to uniform essential boundary conditions on \(\Gamma_2\) for the Imaginary field, the dofs located on that boundary are deleted from the problem via the lambda function remove_dofs_from_problem.
Function Example::assembleSystem() is responsible for evaluating linear and bilinear forms for the problem and assembling the system to be solved
where the wave-number \(k\) has a default value of 90 and can be determined by the user via command line option -k as dictated by the lines below
Thereafter, five lambda functions are determined
that are going to be used as pointer functions in the rest of the function and explained in more detail later.
Moreover, in Example::assembleSystem() operators are pushed to different pipelines managed by the common Pipe Line object pipeline_mng
when operators are pushed by invoking getOpDomainLhsPipeline(), they will be set to be operating on Domain elements and assembling on the LHS of the system of equations. When operators are pushed by invoking getOpBoundaryLhsPipeline() and getOpBoundaryRhsPipeline(), they will be set to be operating on Boundary elements and assembling on the LHS and RHS, respectively.
Two lambda functions set_domain and set_boundary are dedicated to push operators to Domain and Boundary pipelines respectively.
In set_domain lambda function, operators are pushed only in Domain LHS Pipeline. For 2D elements, such as those used in the present tutorial, a pre-processing operation has to be applied to evaluate the gradient of the shape functions. For this, the operators below have to be pushed.
where the first operator evaluates the inverse of the Jacobian at each gauss point. Then, this variable is passed to the second operator and for each gauss point the gradient of the shape function is multiplied with the inverse of the Jacobian so that these gradient correspond to the spatial configuration of the element rather than the parent according to the relationship below
\[ \begin{equation} \begin{aligned} (\nabla \phi)_j = \dfrac{\partial \phi}{\partial \xi_i} \dfrac{\partial \xi_{i}}{\partial X_j} \label{eq:twelve} \end{aligned} \end{equation} \]
where \(\xi_i\) are the parent coordinates \(X_j\) are the global coordinates at the gauss point of interest.
Next, the operator pushed is related to treatment of degrees of freedom located at the boundary \(\Gamma_2\) where Essential boundary conditions are applied since the global variable Example::boundaryMarker is passed where all entities located on \(\Gamma_2\) are stored.
This operator acts on dofs of \(p^{\rm{Re}}\) since string "P_REAL" is passed. By pushing this operator with flag true, all indices that correspond to the dofs corresponding to entities in Example::boundaryMarker that lie on the boundary are set to -1. This will prevent the next operators to assemble the stiffness matrix to rows-columns combination corresponding to those dofs. If flag false was chosen, all the indices corresponding to dofs corresponding to entities located to all the boundary except those in Example::boundaryMarker would be set to -1.
Thereafter, bilinear forms for gradients for \(p^{\rm{Re}}\) and \(p^{\rm{Im}}\) as shown at the two diagonal sub-matrices in \eqref{eq:ten}
\[ \begin{align} \label{eq:thirteen} -{\int_{\Omega}} \nabla \phi_i \nabla\phi_j {\rm{d}}\Omega,\quad -{\int_{\Omega}} \nabla \psi_i \nabla\psi_j {\rm{d}}\Omega \end{align} \]
are evaluated by pushing the next two Operators
where for the first and second push correspond to the first and second integral presented in \eqref{eq:thirteen}. Moreover, OpDomainGradGrad stands for an alias for the OpGradGrad template specialisation
determined in the beginning of the file, where DomainEleOp is also an alias for User Data Operator from Face Elements also determined in the beginning of the file as
Furthermore, the lambda function beta that returns -1 is passed as pointer function so that it will multiply the integral such that it will be assembled with the negative sign as shown in \eqref{eq:thirteen}.
Thereafter, the operator OpDomainMass is pushed twice to the domain LHS pipeline
where the first push operates on \(p^{\rm{Re}}\) rows and cols and the second push operates on \(p^{\rm{Re}}\) rows and cols. These operators will be used from the domain element when the solver will invoke the pipeline to evaluate the mass matrices located on the diagonal sub-matrices in \eqref{eq:ten}
\[ \begin{align} \label{eq:fourteen} k^2{\int_{\Omega}} \phi_i \phi_j {\rm{d}}\Omega,\quad k^2{\int_{\Omega}} \psi_i \psi_j {\rm{d}}\Omega \end{align} \]
Also, the OpDomainMass is an alias of the specialisation of the form integrator template OpMass declared in the beginning of the file
that is of element operator type DomainEleOp similar to the OpDomainGradGrad form integrator shown before. Moreover, in both pushes of OpDomainMass, the lambda function k2, that returns the input of square of wave-number \(k\), is passed as pointer function in order to multiply the mass matrix by \(k^2\) as shown in \eqref{eq:fourteen}.
After all form integrators have been pushed to the Domain LHS pipeline, the dofs that were marked in order not to be used located on \(\Gamma_2\) so that the next pipeline will receive the dofs conditioning in its virgin configuration. This is achieved by pushing operator OpUnSetBc as
At the end of lambda function set_domain, the integration rule for the Domain element for LHS is determined as
In set_boundary lambda function, operators are pushed to the Boundary LHS and RHS pipelines. Initially, for LHS Boundary pipeline the dofs corresponding to entities contained in Example::boundaryMarker Range variable for \(p^{\rm{Re}}\) (located on the \(\Gamma_2\) boundary) are marked not to allow any assembly of the bilinear forms pushed in the pipeline.
Thereafter, the mass matrix type bilinear form integrated on \(\Gamma_1\) boundary
that corresponds to imaginary rows and real columns ("P_IMAG", "P_REAL") presented in \eqref{eq:ten} and given by the formula
\[ \begin{align} \label{eq:fifteen} k{\int_{\Gamma_1}} \psi_i \phi_j {\rm{d}}\Gamma_1 \end{align} \]
where lambda function kp is passed as pointer function to multiply the bilinear form by \(k\) as shown in \eqref{eq:fifteen}. Operator OpBoundaryMass is an alias of bilinear form template specialisation, OpMass, determined in the top of the file as
where the difference with the alias operator previously presented, OpDomainMass, is that the present template specialisation acts on the boundary element operator , EdgeEleOp, determined also at the top of the file as
The next operator push is the same, OpBoundaryMass, that now acts on the real rows and imaginary columns
that evaluates and assembles the bilinear form
\[ \begin{align} \label{eq:sixteen} -k{\int_{\Gamma_1}} \phi_i \psi_j {\rm{d}}\Gamma_1 \end{align} \]
as shown in \eqref{eq:ten} and lambda function km is passed in order to multiply \(-k\) as presented in \eqref{eq:sixteen}. Once all the operators for the Boundary LHS pipeline operating on \(\Gamma_1\) are pushed, the marked dofs have to be release so that the dofs conditioning will be passed intact to the next pipeline and achieved by pushing OpUnSetBc
Essential boundary conditions are also applied following \eqref{eq:eleven} but assumed to have both side multiplied by -1. Initially, operator OpSetBc is now used by setting false flag so that now the rest of the boundary except for \(\Gamma_2\) is now marked not to allow for assembly as
Then the mass bilinear form integrator is pushed using beta lambda function to multiply the integral by -1.
and then the marked boundary is released again by
For setting the RHS linear form the boundary is appropriately marked as in the case for the bilinear form corresponding to the essential boundary conditions but now for the Boundary RHS pipeline as
then the linear form is pushed with lambda function beta so that the integral presented in the RHS in \eqref{eq:eleven} is multiplied by -1
where operator OpBoundarySource is an alias of the template specialisation OpSource assigned in the beginning of the file
and then marked boundary dofs are released again
Finally, integration rules are set for RHS and LHS for Boundary element.
The last three functions invoked in Example::runProblem() are
that each involve solving the system of linear equations using KSPSolver, printing the results for the two fields P_REAL and P_IMAG and checking convergence of the system respectively.
The implementation of these three functions is not discussed in the present tutorial as it is not the focus as discussed in the notes in the beginning of the tutorial. Description of such functions will be discussed in other tutorials.
In order to run the program that we have been discussing in this tutorial, you will have to follow the steps below
helmholtz is located. Depending on how you install MoFEM shown in this page Installation with Spack (Scripts), going to the directory would be something similar to thisgeometry.cub presented in Figure 2 generated in the open source code CUBIT is partitioned in to parts and generated the partitioned mesh part.h5m with boundaries and domain corresponding to \(Gamma_1\) and \(Gamma_2\) presented in Figure 1. In the second line, program is run using two processors (the same number of partitions) with fourth order polynomial of approximation and \(k = 90\).
out_helmholtz.h5m, is generated. To convert the results from .h5m format into .vtk out_helmholtz.vtk file is openned in freely available postprocessing software the calculator solver must be used to evaluate from the solution of the fields P_REAL and P_IMAG by setting the name Intensity in the Result Array Name field and calculating the wave amplitude as \(\sqrt{\left(p^{\rm{Re}}\right)^2 + \left(p^{\rm{Im}}\right)^2}\) by substituting Result Array Name. The associated results are presented in Figure 3.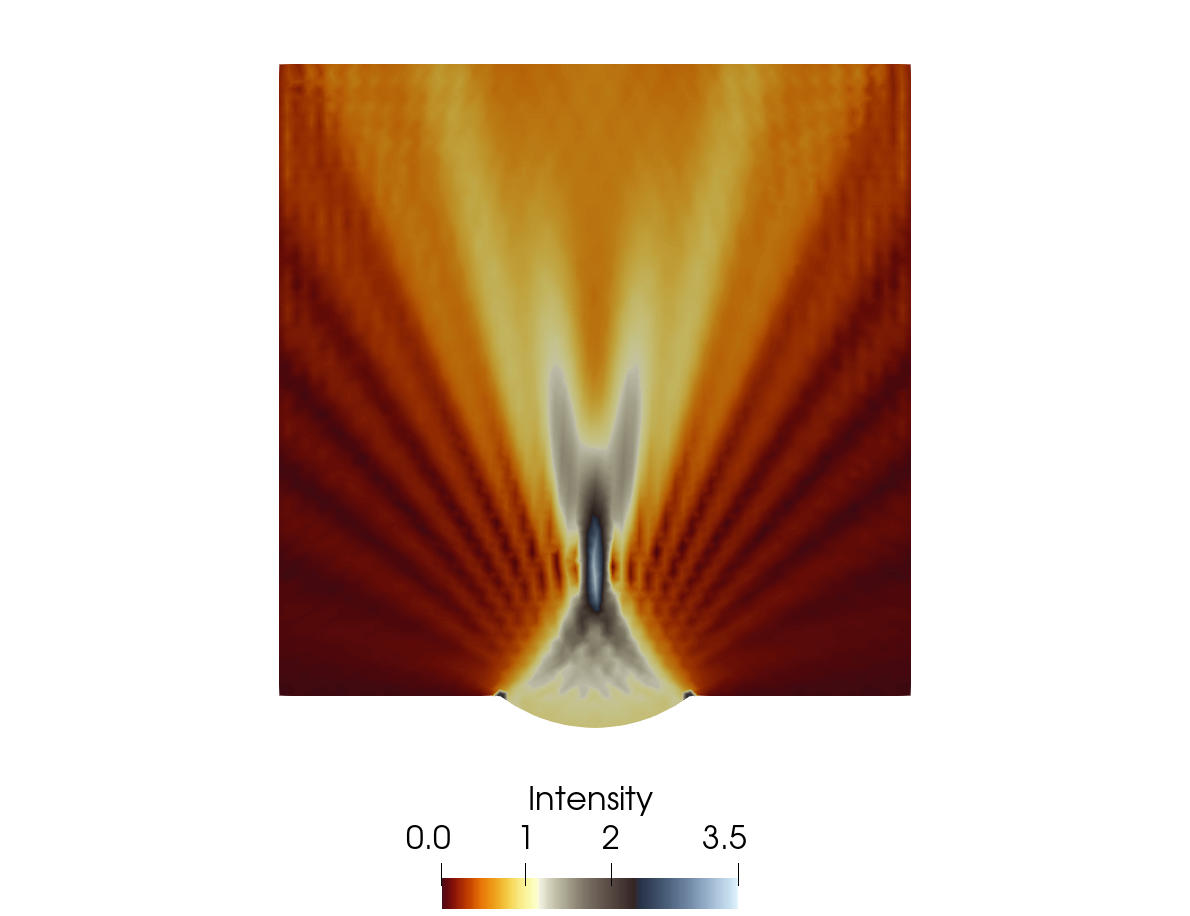
compiling the series of 100 files generated the video presented in Figure 4 will be generated

