 |
v0.14.0 |
 |
v0.14.0 |
This tutorial's motivation is to show how finite element is implemented using basic blocks, like the Lego block where one can combine them in arbitrarily, restricted only by his or her imagination. That is not short and compact code, where PDE can be in single line, but code which can be modified and changed in a way that was not imagined by developers.
This tutorial presents in detail a number of basic Finite Element processes implemented in MoFEM through a user module implementation that solves a simple linear elastic problem. The aim of this presentation is to facilitate new developers to familiarise themselves with certain practices and formulations regarding finite element processes and mesh information manipulation. Readers are encouraged to read MoFEM Architecture, FUN-2: Hierarchical approximation and FUN-0: Hello world before starting the present tutorial. Initially, generation of a mesh is presented and then the module developed for this tutorial is dissected. Finally, code run and post processing of the results are discussed.
The linear elastic problem modelled here is an orthogonal parallelepiped of dimensions \(1.0\times1.0\times4.0 \,\,\rm{m}\), subjected to a uniformly distributed normal traction \(\bar t\) on one face while its opposite face being simply supported. The geometry of the problem is schematically presented in Figure 1. Boundary conditions are applied on the two faces with both edges equal to \(1\,\,\rm m\). Vertical displacements (along z direction) along the whole area of the bottom face are restricted. To prevent rigid body motion, one of the bottom corners displacements along the x and y direction are restricted by the supports numbered 3 and 2 presented in Figure 1, respectively. Finally, displacements along y direction is restricted at a different corner of the bottom face by the support number 1 to prevent rigid body rotation.
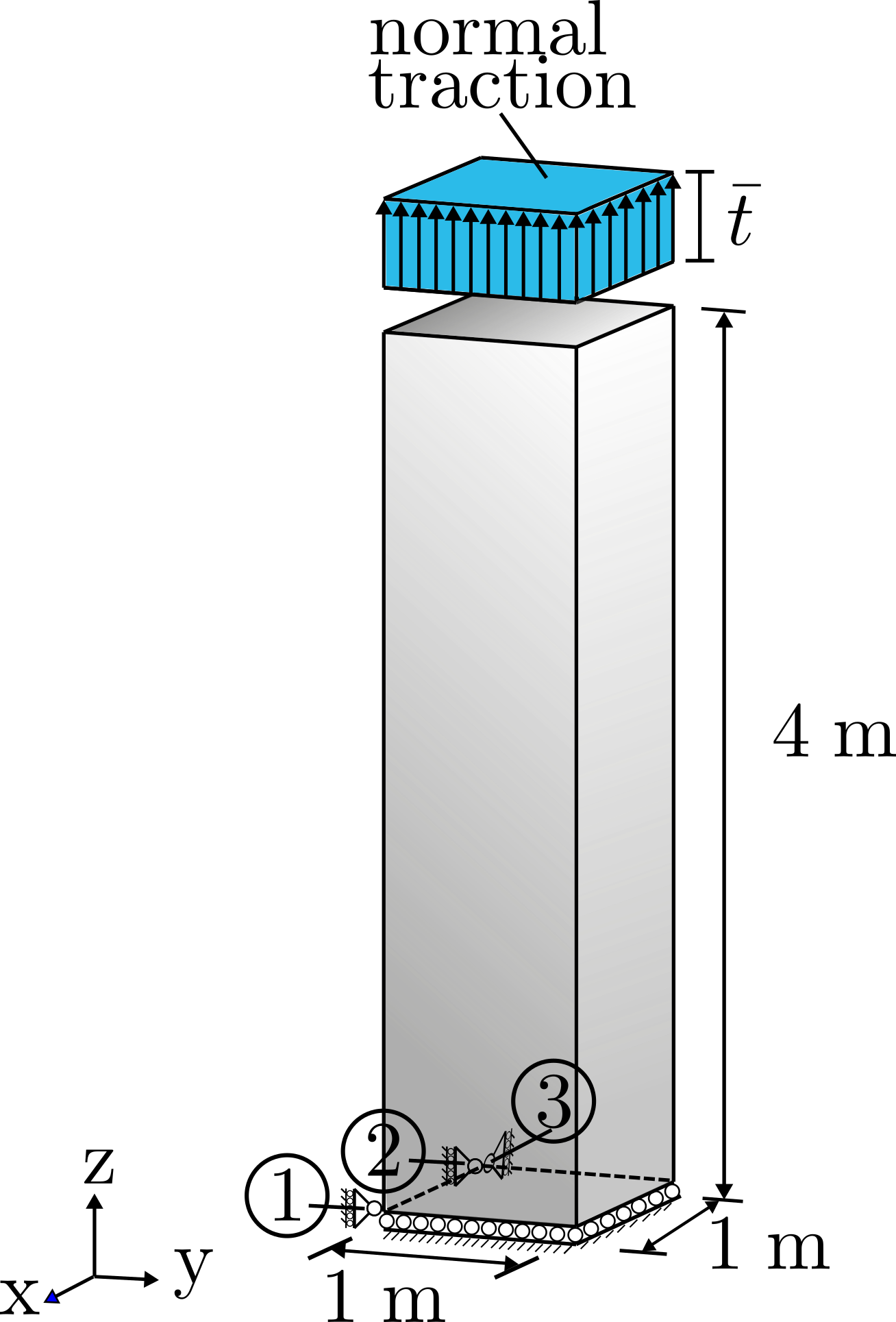
The boundary conditions where chosen to allow the body to deform freely on both horizontal directions. In this way, verification will be possible by checking the match between Poisson ratio recovered by the analysis results with the one used as input as a material parameter. Since only normal tractions are applied on the top face, no bending will occur along the faces parallel to the z axis and therefore no extra support is needed along the bottom edge connecting support 1 and 2.
Particular features associated to mesh input to solve the problem described here will be presented next.
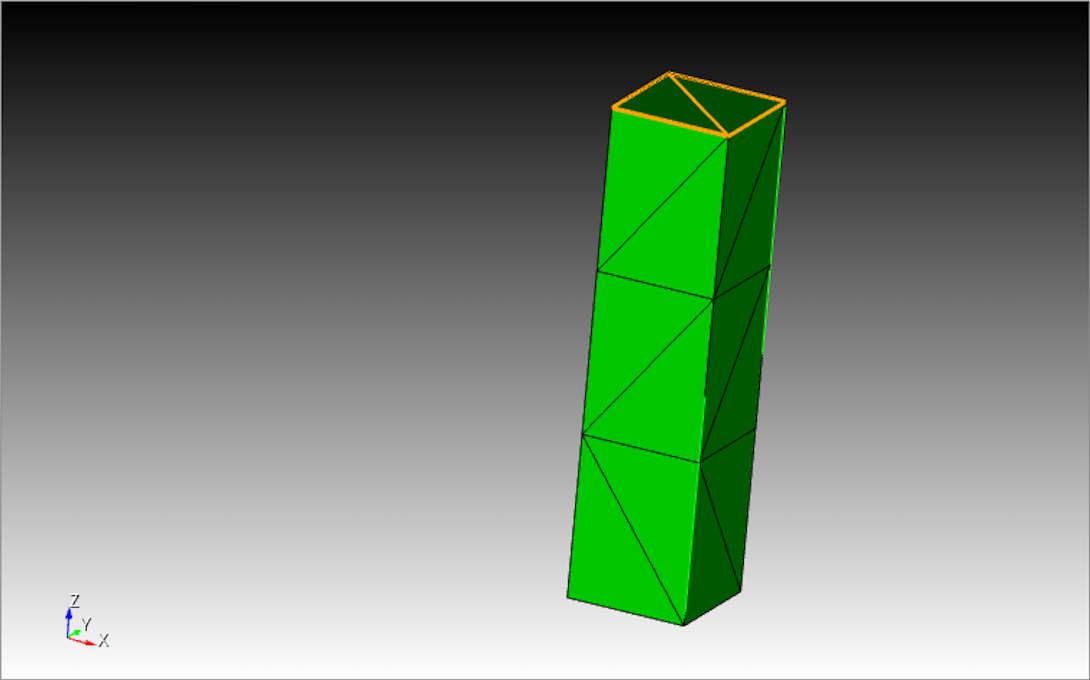
The user module presented here is associated with a specific mesh input. Therefore, mesh generation process is briefly presented focusing only on the steps that are closely linked to the module implementation. There is no intention to provide detail guidelines for using the mesh generator. Mesh generators that can be used to run analyses in MoFEM are Salome, GMsh and Cubit. Mesh features presented here are identical to those found in all three aforementioned software packages.
The mesh presented in Figure 2 corresponds to the geometry of the problem illustrated in Figure 1. However, it should be noted that the mesh generator as well as MoFEM do not require a particular choice of units. Instead, the user is responsible to be consisted with her/his own choice of units for any input parameter.

To prescribe the boundary conditions for the generated mesh presented in Figure 1, a number of blocks must be added to the mesh. To prescribe the restriction on the vertical displacements on the bottom face and the normal traction on the upper face, surface blocks 1 and 3 are added on the corresponding faces as presented in Figure 3 and Figure 4, respectively. Moreover, to assign the displacement restrictions represented by rollers 1, 2 and 3 in Figure 1, vertex blocks have to be added as presented in Figure 5 and Figure 6.



No specific boundary conditions are applied through the mesh generator. To achieve prescription of boundary conditions, certain mesh regions have to be numbered and characterised as ''Blocks''. As explained earlier, block feature exists in Salome, GMsh and Cubit. Therefore, this feature is not restricted to the particular choice of mesh generator. MoFEM user module executable will read the mesh input file and apply boundary conditions (see Sections Mesh block handling and ApplyDirichletBc). As an example, a simple journal script which can be used in Cubit to generate the mesh is found below
reset # Geometry brick x 1 y 1 z 4 # Mesh preparation and generation volume 1 scheme tetmesh volume 1 size auto factor 10 mesh volume 1 block 1 surface 2 block 2 vertex 7 block 3 surface 1 block 4 vertex 6 # Boundary condition # The boundary condition for this problem is defined in the source code # Save the model to *.cub file which will be used in MoFEM code save as "Users/username/mofem_install/um/build/basic_finite_elements/simple_elasticity/cubit.cub" overwrite
The header file included in the user module are presented below.
Initially, MoFEM and PETSc has to be initialised through the code line below
and now PETSc objects can now be declared. As discussed in MoFEM Architecture article, PETSc objects are used to solve the large computational problem of the system of linear equations.
To create the mesh database and an interface to interact with it, the following piece of code is included
MoFEM database is created along with an interface object that will be used as a mean to interact with MoAB database
This interaction is schematically presented as the interaction of level 1 and 2 in Figure 7 on the right hand side.
Moreover, the Discrete Manager that is the PETSc implementation within MoFEM has to be register to PETSc (schematically presented as interaction of levels 1 and 2 on the left hand side in Figure 7)
Interaction of levels 2 and 3 is going to be described in Section Accessing simple interface.
To read data from the command line when executing the program the lines below are introduced
A pointer to an object of type simple_interface is declared.
The second line of code creates a link between simple_interface and m_field interface (schematically presented in Figure 7 as the interaction of levels 2 and 3 by the left hand side arrow).
Interface simple_interface has a number of functions implemented that allows the user to build and manipulate PETSc, MoAB core and MoFEM core databases. For instance, using the code below the mesh file is loaded and information of the mesh is passed to MoFEM database.
Fields of user's interest can be introduced to the MoFEM database through simple_interface object as presented below for the shape functions field in our 3D domain.
By using MoFEM::Simple::addDomainField function the name of the field chosen by the user can be introduced (in this case the name chosen is U). The space chosen to operate is H1 and the type of shape functions is chosen through the key-word AINSWORTH_LEGENDRE_BASE are Legendre polynomials proposed by Ainsworth and Coyle. Finally, the hard-coded number 3 determines the dimensions of the degrees of freedom related to each shape functions. Here, this number is 3 since it is a displacement field in a 3D space. Should the unknown field be pressure, then the hard-coded number will be 1 instead of 3 since pressure always has one dimension. Furthermore, the order of the approximation field is introduced through function MoFEM::Simple::setFieldOrder. As explained earlier, the order of the approximated field can be chosen and the appropriate Hierarchical shape functions will be taken into account accordingly.
Other types of fields can also be introduced to MoFEM database. For instance, an error field can be introduced to evaluate the error variance of the solution throughout the domain. There will be explicit presentation of introduction of other fields in next tutorials.
The blocks numbered 1, 2, 3 and 4 (defined in Section Mesh input) will now be used to apply boundary conditions. First, four Range objects (that are part of MoAB library) are declared for each block
By using the MoFEM core interface m_field, we loop through all meshSets in our MoFEM m_field through the macro _IT_CUBITMESHSETS_BY_BCDATA_TYPE_FOR_LOOP_(m_field, BLOCKSET, bit) as
the identity of each meshSet is found as
the id values correspond to the block numbering presented in Section Mesh input. When the value of id is equal to 1, 2, 3 or 4 boundary conditions are prescribed following the schematic in Figure 1.
For id equal to 1, the meshset is copied to object fix_faces through the MoAB function
were the hard coded number 2, refers to the dimension of entity under consideration which in this case is a face. Numbers 0, 1 and 3 correspond to vertices, edges and volumes, respectively.
Since we are interested in prescribing all degrees of freedom lying along the faces, we need to copy all corresponding entities i.e. vertices and edges, to the fix_faces object. This can be achieved by using the MoAB function get_adjacencies that provides information for the entities adjacent to the input meshset (in this case fix_faces). To implement this, another Range object with name adj_ents is created where all the information of the adjacent entities are going to be copied as presented below.
Similar to the case of function get_entities_by_dimension, hard coded integers indicate the type of entities under consideration. Thereafter, all information passed to the new Range object adj_ents is copied to fix_faces object through the MoAB function merge as
For the vertex type meshsets, no adjacencies are needed since only the degrees of freedom associated to each block is going to be prescribed. Therefore, invoking get_entities_by_dimension function is sufficient.
For the case of the block of the upper face (id = 3), only the degrees of freedom associated to the face are needed. Since the traction is uniform and normal to the upper surface, it can be implemented as pressure and therefore its implementation requires only degrees of freedom associated to the face as presented in section `‘Application of boundary conditions’'.
Finally, the rest of blocks are of vertex type and there is no need to search for adjacencies since only the degrees of freedom at those points are needed to be prescribed.
All problems tackled by user modules proceed with the same workflow for construction of the FEM solution. The workflow implemented in MoFEM is schematically presented in Figure 8 and consists of Definition,

Definition process encompasses creation of stencils of finite elements, fields and problems that are going to be used for the problem solution. Field stencils include name, dimension and order and are defined as
For the elements, the stencil includes element's name, dimension, type of fields that are going to be approximated in this element and the location of the element that the fields operate (volume, boundary or skeleton). Each kind of element used needs a different kind of stencil to be defined.
For reasons that will be apparent in Section OpPressure, we will apply traction boundary conditions through a new element. Since this element is unknown to the simple interface structure we need to explicitly define the element to be included in m_field
Initially, the new finite element type with name is added to MoFEM core database through the function add_finite_element("PRESSURE"), where the string "PRESSURE" used as input is the name that we chose to call the new element. Then, the row and col field information of the "PRESSURE" element are set to be those of "U" type. Furthermore, the list of fields that are associated with "PRESSURE" element listed in the elements data is then set to be only the "U" type field. In a more complicated case, more than one fields can be added to the data, row and col structures of a finite element. Similarly, definition of each problem stencil consists of problem's name and the stencils of the various elements previously presented and are defined using the code lines below
Before defining a problem, all kinds of elements used have to be previously defined.
The new `‘PRESSURE’' finite element has to be explicitly added to DMMoFEM since it was not created through simple_interface. Hence, a DM object is declared and it is set to point to the DMMoFEM create by the interface as
and then the `‘PRESSURE’' finite element is going to be added to DMMoFEM as
This is schematically illustrated as the interaction of levels 2 and 3 on the left hand side of Figure 7. Then all information introduced to DMMoFEM manager is partitioned
This has to be explicitly defined in order to be able to solve the problem in parallel computing where matrix assembly, linear system of equations and mesh is distributed between processors.
Then, fields and finite elements declared through simple_interface are built (second stage presented in Figure 8).
First, the dimension and order of fields according to the specific input chosen is added to the field. In this case, the approximation field of Hierarchic shape functions of Ainsworth and Coyle Legendre polynomials type of order 3 and dimension 3 will be set to the field.
Thereafter, finite elements are built i.e. entities of the finite elements are linked to the field components that were previously built and the order of approximation is set to each entity.
entities associated with the user defined `‘PRESSURE’' finite element have to be explicitly added to the finite element
Then to build all information regarding the element connectivities, and fields associated to element entities into MoFEM core, the function below is invoked.
MoFEM is designed such that approximation fields definition, FE element declaration, FE element definition and FE implementation is explicitly disentangled. That gives us great flexibility allowing for combining individual parts of the code in a countless number of variations.
Implementation FE element can be done on range of levels of abstractions. Here we present implementation which introduces the concept of User Defined Operator. Using its implementation is not constrained to finite element shape or approximation base of fields. In case of coupled or mix formulation, it enables to break down complex code into smaller easy sub-tasks. Here we only introduce basic concepts of this technology.
To create stiffness matrices and apply boundary conditions we will need to finite element instance and attach User Defined Operators (UDOs). For the stiffness matrix evaluation a new shared pointer elastic_fe is instantiated to build elastic finite element instance and a UDO is pushed to the elastic finite elements
schematically presented in Figure 9.
It is important to state that each instance of the structure of elastic finite element pointed by shared pointed elastic_fe carries with it the operator OpK. Element can have sequence of operators, see for example COR-3: Implementing operators for the Poisson equation.
To apply the traction boundary conditions, shared pointer pressure_fe is instantiated and then the operator OpPressure is attached to it to prescribe the traction boundary conditions.
Finally, to prescribe the Dirichlet boundary conditions, the shared pointer fix_dofs_fe is instantiated as a ApplyDirichletBc that is inherited from MoFEM::FEMethod type (which lies within the class that are in the finite elements family within MoFEM) as
The Ranges of fix_faces, fix_nodes and fix_second_node are given as input to the constructor of ApplyDirichletBc to provide the mesh information regarding the location of the degrees of freedom that will be prescribed.
Implementation of OpK, OpPressure and ApplyDirichletBc is presented in Section User Defined Operators (UDOs). A more general implementation for application of boundary conditions will be presented in future tutorials.
In this example the KSP solver provided by PETSc is used. Initially, finite elements are pushed to the discrete manager and set KSP operators for assembling the stiffness matrix.
Then, right hand side vector is evaluated and KSP operators are set to handle it.
Thereafter, stiffness matrix A, vector of degrees of freedom x and right hand side vector f are declared and associated to the Discrete Manager DM
Thereafter, members of finite elements instances are set to point to the aforementioned objects
Now all finite elements are prepared to be iterated (all operators have been pushed to the elements and their members point to the structural problem A, f and x objects) in order to Assembly the problem, i.e. the third part of the work flow presented in Figure 8. Now, each element created is iterated to compute and assemble the stiffness matrix and left hand and right hand vectors as
Furthermore, the part of the prescribed degrees of freedom are assembled in the left hand side vector through
Implementation of UDOs associated with pressure_fe and fix_dof_fe are going to be presented in Section User Defined Operators (UDOs).
At this point matrix and two vectors have been assembled and we can now solve our system of linear equations. Solver is declared first and then connected to the MoFEM core as
The solver object operators have to be prepared
and finally the problem is solved
the results are written in left hand side vector x
and all values of degrees of freedom in x are mapped onto mesh entities
To post process numerical results, initially a post processor object of type PostProcVolumeOnRefinedMesh has to be created based on MoAB database
Thereafter, information of the problem solution is passed to the post processor as
where initially a reference mesh is created is created, then field values are added and finally all information related to finite elements such ass stain and stresses are added into the post processor.
Finally, all information introduced to the post processor object is written to an output file (in this case named out.h5m) as presented below
All dynamic memory objects A, x, f and DM that were created have to be destroyed as presented below
to free the heap memory and prevent any memory leaks.
In structural computational mechanics, the relationship to evaluate the element stiffness matrix \(\mathbf{K}\) is given by
\[ {}^{(r,c)}_eK^{\alpha\beta}_{ik} = \int_{\Omega^e} \varphi_{,j}^\alpha D_{ijkl} \phi_{,k}^\beta \, {d\Omega^e} \label{eq:StiffnessIntegral} \]
where \({\Omega^e}\) is the element volume, \({\mathbf {D}}\) is the elastic material stiffness tensor. The row base funcrions and column base functions are represented by \(\pmb\varphi^\alpha\) and \(\pmb\phi^\beta\), respectively. \(\alpha=1,\dots,N^\textrm{row}\) and \(\beta= 1,\dots,N^\textrm{col}\) are indices of base function on row entities and column entities, respectively. \(N^\textrm{row}\) and \(N^\textrm{col}\) are numbers of base funcions on row entity and collumn entity. The differentation is indicated by subscript and index after the comma, as follows
\[ \varphi^\alpha_{,j} := \frac{\partial \varphi^\alpha}{\partial x_j}. \]
where
\[ i,j = 0,1,2 \]
The integration of the element stiffness matrix is broken down into blocks, utilizing the construction of hierarchical approximation basis. For a hierarchical approximation, base DOFs are grouped on vertices, edges, faces and in the volume of the element, see for details to tutorial FUN-0: Hello world. In this tutorial matrix \({}^{(r,c)}_e\mathbf{K}\) is integrated by running over a combination of block, that is indicated by superscripts \((r,c)\) on the left to the matrix \(\mathbf{K}\), where left-subscripts takes values
\[ r,c := \{\textrm{ver, edge, face, vol} \} \label{eq:setI} \]
The element matrix broked down on block subentities cab be represented as follows
\[ {}_e\mathbf{K} = \left[ \begin{array}{cccc} {}^{\textrm {ver ver}}\mathbf{K} & {}^{\textrm {ver edge}}\mathbf{K} & {}^{\textrm {ver face}}\mathbf{K} & {}^{\textrm {ver vol}}\mathbf{K}\\ & {}^{\textrm {edge edge}}\mathbf{K} & {}^{\textrm {edge face}}\mathbf{K} & {}^{\textrm {edge vol}}\mathbf{K}\\ && {}^{\textrm {face face}}\mathbf{K} & {}^{\textrm {face vol}}\mathbf{K}\\ &&& {}^{\textrm {vol vol}}\mathbf{K}\\ \end{array} \right] \label{eq:StiffStiff} \]
Note that only symmetric part is calculated since the element stiffness matrix is symmetric.
The operator called OpK is implemented as a class inheriting class MoFEM::VolumeElementForcesAndSourcesCore::UserDataOperator
Struct's public members are
The first four lines encompass the declaration of matrices used for the calculation of the elements stiffness matrix as presented in Section Element stiffness matrix.
The next line variables are associated to the material stiffness tensor where D is forth order tensor symmetric on two fisrt and two last indices, yOung is the Young's modulus and pOisson is Poisson's ratio. OpK constructor is implemented as follows
where the material stiffness tensor for Hooke material is calculated.
When solving the problem, as presented in Section Solving the problem, all finite elements are looped where this loop invokes the OpK::doWork method of each operator of the finite element. The OpK::doWork method of operator OpK is implemented as follows
The element's column and row data structures as described in `‘Hierarchic approximation’' tutorial are passed to this function as col_type and row_type respectively.
The number of degrees of freedom associated to each structure (which are equal to the length of the column and row) is then passed to variables nbCols and nbRows and checked that they are non-zero
after the element's lengths of row and columns are passed to nbRows and nbCols and checked to be non-zero, memory for the element's stiffness matrix K that is allocated;
Next, integration of element block stiffnes matrxi is executed, explained in \(\eqref {eq:StiffnessIntegral}\), and finally local matrix is assmble into global stiffnes matrix as follows
Lets first see the OpK::iNtegrate implementation that performs the two inner loops described in Section Entity approximation functions of FUN-2: Hierarchical approximation tutorial
The code iterates over integration points, base functions on rows and base functions on columns. The essential part of the code is integration itself,
Note that is equivalent of sub integral (eq:StiffnessIntegral ). Here we group operation in blocks using brackets, that first derivatives of base functions on rows and columns are multiplied yielding tensor of rank 2
and then the tenor of rank two is multiplied by the tenor of rank two, yielding tensor of rank two. Resultant is multiplied by integration weight times volume of the element and added to local element stiffnes matrix. For more information about tenorial operations see FTensor library
Finally, block local stiffness matrix is assembled into global stiffness matrix as follows
The operator created for the "PRESSURE" finite element that is used to evaluate and assign Neumann boundary conditions according to (12) presented in FUN-2: Hierarchical approximation will be presented in detail. The operator is the struct presented below
Initially, vector nF that will contain the boundary condition forces is declared and index i is defined to be used to perform compact operations later discussed
The evaluation of boundary conditions for each element that are applied is performed within the OpPressure::doWork function. The number of degrees of freedom is initially passed to nb_dofs that is used to appropriately resize vector nF.
Thereafter, the number of gauss points associated to the triangular element is assigned to variable nb_gauss_pts
the normal to the face is passed to t_normal variable
Vector t_normal has 3 component (one for each global axis). Its magnitude is equal to the double of the area of the triangle face since FaceElementForcesAndSourcesCore:UserDataOperator:getTensor1Norma() function returns the vector evaluated by the cross product of the vectors having a common origin on one of the faces vertex and their non-coinciding ends located at the other two vertices. This product is the area defined by the parallelogram rule.
Furthermore, t_base vector containing the element's shape functions is initialised
Then, the loop over all gauss points is performed to evaluate the area integral
In the loop, initially the weight of the gauss point is assigned to w
then t_nF that is a pointer to a vector is initialised in a fashion that points to a piece of memory containing three contiguous double values that are in this case the first three elements of the boundary condition vector nF.
Since the t_nF presents this structure of three contiguous elements pointed by each pointer value, we only need to loop over a third of the number of degrees of freedom.
and the within the loop for each t_nF value, the corresponding block of three members of nF can be evaluated as
Index i in the last line operates the for each part of the three elements of nF. So in the first instance, where bb = 0, nF[0], nF[1] and nF[2] are evaluated.
Thereafter, pointers t_nf and t_base are increased, and now they are pointing to the next corresponding bit of memory.
In the second instance, where bb = 1, t_nf(i) operates in the next three elements of nF, i.e. nF[3], nF[4], nF[5] are evaluated and so on.
Each member of nF contains the surface integral presented in (12) of `‘Hierarchical Approximation’' associated to the the corresponding to gauss point gg and degree of freedom 3*bb. The product that is assigned to t_nf(i) involves multiplication of weight w of gauss point gg, the uniformly distributed traction is a scalar pressureVal times the shape function t_base of degrees of freedom encapsulated in bb, times half the vector normal to the surface. The halving of the vector is done to recover the face area that is the double of the vector magnitude as describe previously.
Finally, the values passed to vector nF are then copied to the right hand side vector \r ksp_f that points to vector f presented in Section Solving the problem used for the solution of the system of linear equations.
The class implemented to apply homogeneous Dirichlet boundary conditions named ApplyDirichletBc is presented below
Entities that were previously handled in Section Mesh block handling are assigned through the constructor in public variables fixFaces, fixNodes, fixSecondNode
The homogeneous boundary conditions are then implemented in postProcess() function. Initially, a loop over degrees of freedom is performed through macro `‘for (\_IT\_NUMEREDDOF\_ROW\_FOR\_LOOP\_(problemPtr, dit))’'. Within the loop, the degrees of freedom corresponding to the entities passed to the public variables of the struct are inserted to vector of integers set_fix_dofs through insert function
then this data is pass to a new vector of integers fix_dofs
Thereafter, the stiffness matrix ksp_B and right hand side vector ksp_f structures are constructed
and the left hand side vector x is constructed by copying ksp_f to x and subsequently zeroing it
Invoking function MatZeroRowsColumns the columns and rows corresponding to the prescribed degrees of freedom stored in fix_dofs and the diagonal element is set to unity and the corresponding degrees of freedom in vector x are set to zero.
finally the memory allocated for vector x is freed
To run the code one should change directory to
Then run the command
To visualise results first convert the out put file from .h5m format to a vtk one
then open the .vtk file in ParaView http://www.paraview.org. For example on macOS
Figure 10 shows the ParaView visualisation of the result of the considering problem.

If you have problems with understanding this tutorial or exercises, please contact us on Q&A forum, see link.
The plain program is located in users_modules/basic_finite_elements/simple_elasticity/simple_elasticity.cpp
