- Note
- Prerequisites of this tutorial include FUN-1: Integration on finite element mesh, following SCL-1: Poisson's equation (homogeneous BC), SCL-4: Nonlinear Poisson's equation, VEC-0: Linear elasticity and finally VEC-2: Nonlinear elastic
- Note
- Intended learning outcome:
- nonlinear elasticity
- automatic differentiation
- linearisation
- tangent operators
- discountinuous Galerkin projection
- users modules
This code, after some refactoring and removing handling cohesive interferes and periodic boundary conditions to serve the purposes of the tutorial is based on code used in [71] (doi: https://doi.org/10.1016/j.compstruct.2016.11.059), see Figure Figure 1.
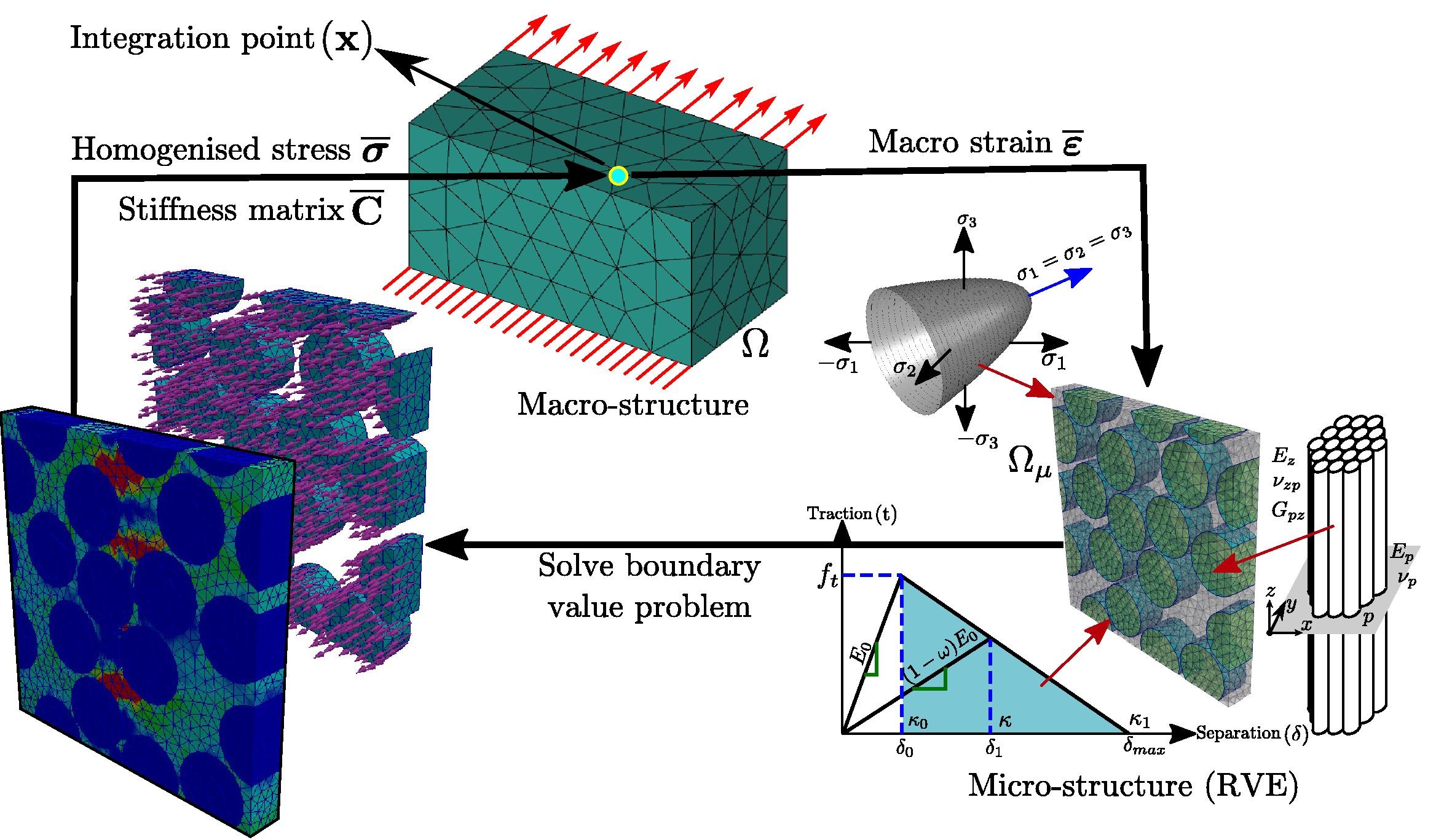
Figure 1: Three-dimensional nonlinear micro/meso-mechanical response of fiber-reinforced polymer composites. Note paraboloidal surface described bewlo.
However, some limitations of the original code are removed, i.e., the code can be used to solve complex practical problems, see tutorial code specification. Note that MoFEM tutorials are dedicated to contributors and developers keen to extend functionality, rather than to end-users.
You can jump immediately into the details of implementation here link. You also might look at ADOL-C implementation (library used for automatic differentiation), see ADOL-C manual.
- Note
- This tutorial utilizes automatic differentiation which is a powerful tool, however, here using it we evaluate hessian which has significant efficiency drawbacks. Despite that code has educational, value. Moreover, enables testing some ideas about plasticity models. Some efficiency drawbacks can be mitigated by parallel processing, however, plasticity is often localized to small regions, which requires load balancing. However current implementation works in parallel, load balancing is not implemented, and this tutorial will benefit from such a feature.
- Todo:
- Fix notation, use bold for vectors and tensors. Commas and dots at the end of equations. Other issues.
Installation
This tutorial is a separate module, located in an independent repository. Users who would like create bespoke solutions for some research or industrial problems would like to create independent repository which is their ownership, licensing and contribution policy. If necessary keep it private. This tutorial is an example of how it can be done.
You can install a module using Spack.pm, which module is an extension to generic user modules. That simplifies use and installation for end users. However for development purposes, you can install the module as follows:
- Clone repository
cd $HOME/mofem_install/mofem-cephas/mofem/users_modules
git clone -b master https://bitbucket.org/mofem/adolc-plasticity.git
- Build module
cd $HOME/mofem_install/mofem-cephas/mofem/users_modules/um-build-Rel*
make rebuild_cache
make -j 4 install
Tutorial program specification
- We provide tutorials for elastoplasticity problems in 2D and 3D on the triangle, quadrilateral, tetrahedron and hexahedron elements. In the 2D case, the code can handle plane stress and plane strain. One source code serves all cases.
- Implementation is generic, dimension agnostic, i.e. code is implemented that dimension of the problem is unknown while implementation, but is known at compile time. Thus we exploit static polymorphism, i.e. C++ templates and partial specialization.
- The type elements, the order of approximate is not known at compile time, is decided at run time. Thus we exploit dynamic polymorphism, i.e. C++ virtual functions.
- Code is assumed to be run in parallel, on distributed mesh. No load balancing if performed, thus we assume that the mesh is balanced.
- Code can handle a "zoo" of different boundary conditions, i.e. Dirichlet, Neumann, and Robin, i.e. spring boundary conditions.
- Code can handle multiple material blocks, and if necessary can be extended to handle material property fields.
- Users can easily add new material models.
- Some points are different approaches between 2D and 3D while post-processing. In the 2D case, we can plot stress and strain on the interior face element, while in the 3D case, we can plot stress and strain volume of the skin, i.e. skin faces. That is a point that we perform branching, i.e. consent expression if a statement is used, at compilation time.
- Note
- That can/should be code extended to large deformations by following the Mieche procedure [55], which utilizes Lie algebra by applying the logarithmic mapping to the left Cauchy-Green deformation tense. This code is based on the additive decomposition of total strain into elastic and plastic parts. Logarithmic strains, also called Hencky strains, are additive, and that is why the Mieche procedure allows the use of the code below in essence in unchanged form. See VEC-2: Nonlinear elastic or ADV-0: Plastic problem for details.
Theory and problem formulation
Introduction
In the following document, we define functions \(\psi(\varepsilon^e,\alpha)\), \(f(\sigma,\overline{\alpha})\) and \(\Psi(\sigma,\overline{\alpha})\) which are free (Helmholtz) energy, yield function and flow potential, respectively. Note that free energy is defined by strains and kinematic internal state variables, whereas yield function and flow potential are defined by fluxes (stress tensor and fluxes work conjugated to internal kinematic state variables). In this formulation, we assume that all functions are convex. From the convexity of free energy emerges the ellipticity of the partial differential equation, which is solved to satisfy the conservation of the linear momentum, i.e. establish equilibrium. The convexity of the yield function guarantees the uniqueness of the return on the plastic surface, and the convexity of the flow potential guarantees positive dissipation, i.e. the second law of thermodynamics is satisfied. For details see [66]. Moreover, in the following implementation is assumed that all functions are smooth enough that appropriate derivatives can be calculated, in particular, we assume that plastic surfaces do not have corners or apexs.
In the following implementation, the implicit scheme is applied to solve a set nonlinear system of equations with unilateral constraints. The admissible stress state is enforced by the Lagrange multiplier method and (Kuhn-Tucker) loading/unloading conditions, see [66].
Following [66] can be shown that plastic loading unloading conditions can be exclusively characterized in terms of trial state
\[ \varepsilon^{e,\textrm{trial}}_{n+1} := \varepsilon_{n+1} - \varepsilon^p_n \]
\[ \alpha^\textrm{trial}_{n+1} := \alpha_n \]
\[ \sigma^\textrm{trial}_{n+1} := \frac{\partial \psi}{\partial \varepsilon^e} (\varepsilon^{e,\textrm{trial}}_{n+1},\alpha_n) \]
\[ \mathbf{\overline{\alpha}}^\textrm{trial}_{n+1} := \frac{\partial \psi}{\partial \alpha} (\varepsilon^{e,\textrm{trial}}_{n+1},\alpha_n) \]
\[ f^\textrm{trial}_{n+1} := f(\sigma^\textrm{trial}_{n+1},\overline{\alpha}_n) \]
then loading/unloading conditions are given
\[ \begin{split} f^\textrm{trial}_{n+1} < 0,\quad\textrm{elastic step}\,\to\,\Delta\gamma_{n+1} = 0 \\ f^\textrm{trial}_{n+1} \geq 0,\quad\textrm{plastic step}\,\to\,\Delta\gamma_{n+1} > 0 \end{split} \]
If first condition is true \(f^\textrm{trial}_{n+1} < 0\), trial stress is solution at integration point. If the second condition is true, plastic strains and values of the internal state variables are calculated using Closet point projection algorithm. For consistency, we also satisfy the condition \(\Delta\gamma_{n+1}f_{n+1}\), at all converged states.
Closet point projection algorithm
Additive strain decomposition
We assume that the total strain is decomposed into elastic and plastic parts, as follows
\[ \varepsilon_{n+1} = \varepsilon^e_{n+1} + \varepsilon^p_{n+1} \]
where \(\varepsilon_{n+1} = \textrm{sym}[ \nabla \mathbf{u}_{n+1}]\) is the total strain, \(\varepsilon^e_{n+1}\) is elastic strain, and \(\varepsilon^p_{n+1}\) is the plastic strain. \(\mathbf{u}_{n+1}\) is displacement at time \(t_{n+1}\).
Constitutive relations
The constitutive relations are defined exclusively through the free energy potential as follows, for the stresses and internal fluxes, respectively
\[ \sigma_{n+1} := \frac{\partial \psi}{\partial \varepsilon^e}\left(\varepsilon^e_{n+1},\alpha_{n+1}\right), \quad \mathbf{\overline{\alpha}}_{n+1} := \frac{\partial \psi}{\partial \alpha}\left(\varepsilon^e_{n+1},\alpha_{n+1}\right) \]
Note that the stresses, i.e. fluxes of linear momentum, are work-conjugated to the strains and the internal fluxes \(\overline{\alpha}\) is work conjugated to the kinematic internal state variables \(\alpha\).
Constraints
The admissible inelastic domain is defined by the yield function
\[ f_{n+1}:=f(\sigma_{n+1},\mathbf{\overline{\alpha}}_{n+1}), \quad f_{n+1} \leq 0 \]
The yield stress could be understood as functional, with zero value implicitly defines the yield surface.
Evolution functions
The flow rule defines the evolution of plastic strains, such that
\[ \mathbf{n}_{n+1}:=\frac{\partial \Psi} {\partial \sigma} \left(\sigma_{n+1},\mathbf{\overline{\alpha}}_{n+1}\right), \quad \Delta \varepsilon^p_{n+1} = \Delta \gamma_{n+1} \mathbf{n}_{n+1} \]
where \(\Delta \gamma_{n+1}\) is the plastic multiplier, and has to be determined that for the plastic process, stress remains on the yield surface, i.e. \(f_{n+1} = 0\). The evolution of internal variables is
also defined consistently by the flow potential, such that
\[ \mathbf{h}_{n+1}:=-\frac{\partial \Psi}{\partial \mathbf{\overline{\alpha}}} \left(\sigma_{n+1},\mathbf{\overline{\alpha}}_{n+1}\right), \quad \Delta \alpha_{n+1} = \Delta \gamma_{n+1} \mathbf{h}_{n+1} \]
Residual
Notting that in computational setting loading increment is finite, If we load the body at some point we will exceed the yield stress, thus we reach an inadmissible state. As a consequence, we have to return to the yield surface and stay on it, while material plastically yields. That task leads to an optimization problem with unilateral constraints [66].
Once we establish that the material plastically flows, by calculating the state for trial stress, which is done individually for each integration point, we solve the optimization problem. The standard procedure is the Lagrange method, which introduces an additional variable, i.e. the Lagrange multiplier, which in this context is called the plastic multiplier, i.e. \(\Delta\gamma\), mentioned above. In some cases, we can associate some physical interpretation to the plastic multiplier, however, in general, it is just a mathematical tool.
Finally, the problem at the integration point boils down to the problem of solving a system of nonlinear equations. We have a whole spectrum of possibilities, including the Newthon-Raphson method, trust region methods, and line searchers, available through the PETSc library and its SNES solver.
To use SNES solver, we need to define the residual and the tangent operator. Here residual is defined as follows
\[ \mathbf{R}_{n+1}^{i}:= \left\{ \begin{array}{c} -\varepsilon^p_{n+1}+\varepsilon^p_n \\ -\alpha_{n+1}+\alpha_n \\ f_{n+1} \end{array} \right\}^i + \Delta\gamma_{n+1}^i \left\{ \begin{array}{c} \mathbf{n}_{n+1} \\ \mathbf{h}_{n+1} \\ 0 \end{array} \right\}^i \]
where \(i\) is the iteration number. The last row of the residual vector has an interpretation of the distance to yield surface and in the process of the solution of the optimization problem, we reduce that distance to the surface, thus naming closes point projection. Residual can be defined in several alternative ways, here we choose the most straightforward naive way to define it, which works well, at least for the problems we tested. From residual, by applying chain derivatives we obtain the tangent matrix, i.e. second quantity required by SNES solver. Tangent matrix is derived as follows
\[ \left[ \begin{array}{ccc} -1+\gamma \left( \frac{\partial\mathbf{n}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} + \frac{\partial\mathbf{n}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial\alpha\varepsilon^p} \right) & \gamma \left( \frac{\partial\mathbf{n}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} + \frac{\partial\mathbf{n}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \alpha} \right) & \mathbf{n} \\ \gamma \left( \frac{\partial\mathbf{h}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} + \frac{\partial\mathbf{h}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial\alpha\partial\varepsilon^p} \right) & -1+\gamma \left( \frac{\partial\mathbf{h}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} + \frac{\partial\mathbf{h}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \alpha} \right) & \mathbf{h}\\ \frac{\partial f}{\partial \sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} + \frac{\partial f}{\partial \mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha\partial\varepsilon^p} & \frac{\partial f}{\partial \mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} + \frac{\partial f}{\partial \sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial\alpha} & 0 \end{array} \right]^i \left\{ \begin{array}{c} \delta \varepsilon^p \\ \delta \alpha \\ \delta \gamma \end{array} \right\} = \mathbf{R}^{i} \]
where \(\left(\varepsilon^p_{n+1}\right)^{i+1}=(\varepsilon^p_{n+1})^i + \delta\varepsilon^p_{n+1}\), \(\left(\alpha^p_{n+1}\right)^{i+1}=(\alpha_n)^i + \delta\alpha_{n+1}\) and \(\left(\Delta\gamma_{n+1}\right)^{i+1} = (\Delta\gamma_n)^i+\delta\gamma_{n+1}\). The quantities proceeded by \(\delta\) are sub increments of the Newton-Raphson method, calculated at series of iterations. Usually, it is assumed free energy split, since is easier to construct a convex function, as follows
\[ \psi(\varepsilon^e,\alpha) = \psi^{\varepsilon}(\varepsilon^e) + \psi^\alpha(\alpha) \]
in that case, linearized residual takes the form
\[ \left[ \begin{array}{ccc} -1+\Delta\gamma \frac{\partial\mathbf{n}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} & \Delta\gamma \frac{\partial\mathbf{n}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} & \mathbf{n} \\ \Delta\gamma \frac{\partial\mathbf{h}}{\partial\sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} & -1+\Delta\gamma \frac{\partial\mathbf{h}}{\partial\mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} & \mathbf{h}\\ \frac{\partial f}{\partial \sigma}\frac{\partial^2 \psi}{\partial \varepsilon^e \partial \varepsilon^p} & \frac{\partial f}{\partial \mathbf{q}}\frac{\partial^2 \psi}{\partial \alpha^2} & 0 \end{array} \right]^i \left\{ \begin{array}{c} \delta \varepsilon^p \\ \delta \alpha \\ \delta \gamma \end{array} \right\} = -\mathbf{R}_n^i \]
Where sub increment of the Newton-Raphson method is calculated as follows
\[ \delta \chi = \left\{ \begin{array}{c} \delta \varepsilon^p \\ \delta \alpha \\ \delta \gamma \end{array} \right\} = - \mathbf{A}^{-1} \mathbf{R}_n^i, \quad \chi^{i+1} = \chi^i + \delta \chi \]
where \(\mathbf{A}\) is the tangent metrix defined above.
- Note
- If would you like to improve residual definition, let us know, and we will be happy to guide you.
Algorithmic tangent matrix
The classical approach to computational plasticity is based on a nested approach, we solve unilateral optimization-constrained problems at the integration point, and then we assemble the global tangent operator, which we use to solve the global problem, of emerging from the conservation of linear momentum.
The global problem is nonlinear, as a consequence of the nonlinear material model, i.e. elastoplasticity. The global problem is computationally expensive, and solving it efficiently using the Newton-Raphson. The Newton-Raphson method promises quadratic convergence, near the solution, however, it requires the calculation of the tangent operator, which is consistent with the residual. In our case, the residual depends on a nested solution, which is also solved by the Newton-Raphson method. To calculate a consistent tangent operator, at the global system level, we need to calculate the change of plastic strain as a function of of change of total strain, which implicitly depends on the change of internal material state variables.
To derive the consistent tangent operator, start with the constitutive equation
\[ \delta \sigma := \mathbf{C}^e(\delta \varepsilon - \delta \varepsilon^p) \]
where \(\mathbf{C}^e = \frac{\partial^2 \psi^e}{\partial {\varepsilon^e}^2}\) and \(\delta \varepsilon = \textrm{sym}[ \nabla \delta \mathbf{u}]\) is change of total strain.
Then we introduce the three operators, for completeness, however, we need only first one for the derivation of system level tangent operator. Mentioned operators have form
\[ \left\{ \begin{array}{c} \mathbf{E}^p \\ \mathbf{L}^p \\ \mathbf{Y}^p \end{array} \right\} \delta \varepsilon = - \mathbf{A}^{-1} \left\{ \begin{array}{c} \Delta\gamma \frac{\partial \mathbf{n}}{\partial \sigma}\mathbf{C}^e \\ \Delta\gamma \frac{\partial \mathbf{h}}{\partial \sigma}\mathbf{C}^e \\ \frac{\partial f}{\partial \sigma}\mathbf{C}^e \end{array} \right\} \delta \varepsilon. \]
The operator \(\mathbf{E}^p\) provides us the infinitesimal increment of plastic strans, as a consequence of the infinitesimal increment of total strain strain. Note that through inverse of the tangent operator \(\mathbf{A}\), the increment of plastic strain is coupled with a change of Lagrange plastic multiplier, i.e. containing infinitesimal increment of stress such that it remains plastic surface. We note that consistent tangent operator is implicitly connected to algorithm, and our choice of definition of the residual.
Taking the above, we can see that we can express an increment of the plastic stain internal fluxes, and plastic multiplier as follows
\[ \delta \varepsilon^p = \mathbf{E}^p \delta \varepsilon,\quad \delta \alpha = \mathbf{L}^p \delta \varepsilon,\quad \delta \gamma = \mathbf{Y}^p \delta \varepsilon \]
Plugin first equation from above into the constitutive equation we obtain
\[ \delta \sigma = \mathbf{C}^e(\mathbf{1} - \mathbf{E}^p)\delta \varepsilon \]
which directly gives us material consistent tangent operator
\[ \delta \sigma = \mathbf{C}^{ep}\delta \varepsilon \]
where \(\mathbf{C}^{ep} = \mathbf{C}^e-\mathbf{C}^e\mathbf{E}^p\). We use \(\mathbf{C}^{ep}\) to assemble the global tangent operator, i.e. the holy grail of computational plasticity.
B-bar method
When material plastic flows, additional constraints are imposed on the finite element deformation, emerging from the flow rule, in particular for J2 plasticity where plastic flow is isochoric, i.e. volume-preserving. That is a case for 3D case and plane strain. In such cases, low-order elements are locking, i.e. elements do not converge fast to the exact solution, fast as Céa's lemma states for elliptic problems, i.e. that the solution error is the best approximation error.
For low-order quadrilateral elements, there are several methods to mitigate the problem. That is reduced integration with hourglass stabilization, selective integration, and the B-bar method. Here we use the B-bar method, whose name comes from the modification finite element differential operator, i.e. \(\mathbf{B}\) operator, in the finite element expression for the stiffness matric \(\int_{V^e} \mathbf{B}^\textrm{T} \mathbf{C} \mathbf{B} \textrm{d}V\). The B-bar added on the top of the \(\overline{\mathbf{B}}\) operator, indicates that the strain axiator of the deformation is averaged on the element, which is equivalent to selective integration. Since the evaluation of constitutive equations are computationally expensive, in particular with automatic differentiation, we use the B-bar method to be more attractive.
The principle of the B-bar method is expressed by the following formula for variation of strain work on stress, i.e.
\[ \delta \mathcal{W} = \int_{V^e} \mathbf{B}^\textrm{T} \sigma \textrm{d}V = \int_{V^e} \delta \varepsilon \sigma \textrm{d}V \approx \int_{V^e} \left[ \delta \varepsilon + \frac{1}{3} \left( (\textrm{tr}[\delta\varepsilon])^\textrm{ave} - \textrm{tr}[\delta\varepsilon] \right)I \right] \sigma \textrm{d}V = \int_{V^e} \overline{\mathbf{B}}^\textrm{T} \sigma \textrm{d}V \]
, where is an average of the trace of the strain tensor, i.e.
\[ (\textrm{tr}[\delta\varepsilon])^\textrm{ave} = \frac{1}{V^e} \int_{V^e} \textrm{tr}[\delta\varepsilon] \textrm{d}V. \]
where \(V^e\) is the volume of the element.
The above formula is implemented using tensorial notation, rather than matrix notation, typical for traditional nodal-based finite element codes. See file ADOLCPlasticity.cpp and snippet below.
template <int DIM>
const int nb_integration_pts, double *w_ptr,
const auto nb_dofs = data.getFieldData().size();
const auto nb_bases = data.getN().size2();
storage.resize(nb_integration_pts, 6 * nb_dofs, false);
auto get_ftensor2_symmetric = [&](const int gg, const int rr) {
};
auto calc_base = [&]() {
auto t_t2_diff = get_ftensor2_symmetric(0, 0);
for (auto gg = 0; gg != nb_integration_pts; ++gg) {
auto t_diff = data.getFTensor1DiffN<DIM>(gg, 0);
for (auto b = 0; b != nb_dofs / DIM; ++b) {
t_grad(N0,
J) = t_diff(
J);
t_t2_diff(
i,
j) = (t_grad(
i,
j) || t_grad(
j,
i)) / 2;
++t_t2_diff;
t_grad(N1,
J) = t_diff(
J);
t_t2_diff(
i,
j) = (t_grad(
i,
j) || t_grad(
j,
i)) / 2;
++t_t2_diff;
if constexpr (DIM == 3) {
t_grad(N2,
J) = t_diff(
J);
t_t2_diff(
i,
j) = (t_grad(
i,
j) || t_grad(
j,
i)) / 2;
++t_t2_diff;
}
++t_diff;
}
}
return get_ftensor2_symmetric(0, 0);
};
auto calc_vol = [&](auto &&t_t2_dff) {
std::vector<double> vol(nb_dofs, 0);
for (auto gg = 0; gg != nb_integration_pts; ++gg) {
for (auto b = 0; b != nb_dofs; ++b) {
vol[b] += w_ptr[gg] * t_t2_dff(
i,
i) / DIM;
++t_t2_dff;
}
}
double sum = 0;
for (auto gg = 0; gg != nb_integration_pts; ++gg) {
sum += w_ptr[gg];
}
}
return vol;
};
auto make_b_bar = [&](auto &&vol) {
auto t_t2_diff = get_ftensor2_symmetric(0, 0);
for (auto gg = 0; gg != nb_integration_pts; ++gg) {
for (auto b = 0; b != nb_dofs; ++b) {
const auto trace = t_t2_diff(
J,
J) / DIM;
++t_t2_diff;
}
}
return get_ftensor2_symmetric(0, 0);
};
return b_bar ? make_b_bar(calc_vol(calc_base())) : calc_base();
};
As a result of the above code, we obtain the tensorial base functions, which are used to evaluate the stiffness matrix and the right-hand side vector. For the latter case, code is shown in the snippet form ADOLCPlasticity.hpp below
template <int DIM, typename AssemblyDomainEleOp>
double *w_ptr = &(OP::getGaussPts()(DIM, 0));
auto t_diff = MakeB::getFTensor2SymmetricDiffBase(
data, baseStorage, commonDataPtr->bBar, OP::getGaussPts().size2(), w_ptr,
auto t_stress = getFTensor2SymmetricFromMat<3>(commonDataPtr->stressMatrix);
const auto vol = OP::getMeasure();
auto t_w = OP::getFTensor0IntegrationWeight();
for (int gg = 0; gg != OP::nbIntegrationPts; gg++) {
double alpha = vol * t_w;
for (int bb = 0; bb != OP::nbRows; ++bb) {
OP::locF[bb] += alpha * (t_stress(
i,
j) * t_diff(
i,
j));
++t_diff;
}
++t_w;
++t_stress;
}
}
- Note
- Another method for resolving the issue with locking would be adding a bubble function on the element, which is a natural way in MoFEM, look to ADV-0: Plastic problem to see how this can be done. You can also look at VEC-0: Linear elasticity to learn how bubble could be efficiently by removing block diagonal entries from the stiffness matrix using the Schur complement and block solver.
Material models
Each material model is a class derived from the base class ADOLCPlasticity::ClosestPointProjection. Each class has three abstract methods, which must be implemented by the user. That is ADOLCPlasticity::ClosestPointProjection::freeHemholtzEnergy, ADOLCPlasticity::ClosestPointProjection::flowPotential and ADOLCPlasticity::ClosestPointProjection::yieldFunction.
If a new model is implemented, it must be registered in the factory, see and follow the pattern below from adolc_plasticity.cpp
enum MaterialModel {
VonMisses,
VonMissesPlaneStress,
Paraboloidal,
LastModel
};
const char *list_materials[LastModel] = {"VonMisses", "VonMissesPlaneStress",
"Paraboloidal"};
PetscInt choice_material = VonMisses;
LastModel, &choice_material, PETSC_NULL);
switch (choice_material) {
case VonMisses:
cpPtr = createMaterial<J2Plasticity<3>>();
break;
case VonMissesPlaneStress:
"VonMissesPlaneStrain is only for 2D case");
cpPtr = createMaterial<J2Plasticity<2>>();
break;
case Paraboloidal:
cpPtr = createMaterial<ParaboloidalPlasticity>();
break;
default:
}
cpPtr->integrationRule = [](
int,
int,
int p) {
return 2 * (p - 2); };
- Todo:
- For simplicity we predefine one model to the mesh, however, using MoFEM::MeshsetsManager it is possible to assign different models to mesh blocks baes on the block name. We should implement this extension. Block names can be set in Cubit, gMesh, or Salome. In particular MED format can handle block names.
Auxiliary functions
The class has two auxiliary virtual functions, ADOLCPlasticity::ClosestPointProjection::addMatBlockOps, and ADOLCPlasticity::ClosestPointProjection::setParams. Both are optional and can be used to read material properties from mesh blocks or to set material properties. Using this functionality more complex cases can be handled, for example, by reading material properties from a stochastic field.
Reading of material properties from mesh blocks is implemented as an example for von Misses material model, see ADOLCPlasticity::J2Plasticity<3>::addMatBlockOps and ADOLCPlasticity::J2Plasticity<3>::setParams.
J2 plasticity
Von Mises yield function, know also as J2 plasticity, also called HMH plasticity after Huber, Mises and Hencky, who invented pressure-independent strength criterion independently. This model is useful to describe the behavior of a large class of metals.
Free energy density
Free energy density has form
\[ \psi(\varepsilon^e, \alpha, \beta) = \frac{1}{2} \lambda \textrm{tr}[\varepsilon^e]^2 + \mu \varepsilon^e : \varepsilon^e + \sigma_y\alpha + \frac{1}{2} \phi H \alpha^2 + \frac{1}{2} (1-\phi)K \beta^2 \]
where \(\lambda\) and \(\mu\) are Lame'e parameters, \(\sigma_y\) is yield stress, \(\varepsilon^e\) is elastic strain \(\alpha\) is the internal variable associated with isotropic hardening and \(\beta\) is the internal variable associated with kinematics hardening. \(\phi\) is the fraction controlling how the amount of kinematic and isotropic hardening is useful for studying the Bauchinger effect, i.e. plastic hysteresis under cyclic loading.
In general, such a function needs to be convex, which yields elasticity of the problem, and the uniqueness of the solution. Here we restricted implementation to polyconvex form, i.e. that each term separated by addition is convex. That separates in an additive way strains and internal variables, as stated in Introduction, and exploited while assembly the nested tangent operator. Models in small strains, since a symmetric gradient of displacements is used, are invariant to infinitesimal rotations, which provides objectivity to the problem in infinitesimal cases. Also, note that the model can be easily extended to anisotropic cases.
The code for which the above function is implemented is given below from ADOLCPlasticityMaterialModels.hpp
auto p_lambda = mkparam(
lambda);
auto p_phi = mkparam(
phi);
auto p_sigma_y = mkparam(
sigmaY);
auto t_voight_total_strain = getFTensor1FromPtr<6>(&a_sTrain[0]);
auto t_voight_plastic_strain = getFTensor1FromPtr<6>(&a_plasticStrain[0]);
auto t_voight_internal_tensor =
getFTensor1FromPtr<6>(&a_internalVariables[1]);
tTotalStrain(
i,
j) = t_voight_strain_op(
i,
j, Z) * t_voight_total_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_plastic_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_internal_tensor(Z);
tElasticStrain(
i,
j) = tTotalStrain(
i,
j) - tPlasticStrain(
i,
j);
tR = tElasticStrain(
i,
i);
a_w = 0.5 * p_lambda * tR * tR +
p_mu * (tElasticStrain(
i,
j) * tElasticStrain(
i,
j));
a_w +=
a_internalVariables[0] * p_sigma_y +
0.5 * p_phi * p_H * (a_internalVariables[0] * a_internalVariables[0]);
a_w += (0.5 * (1 - p_phi) * p_K) *
(tInternalTensor(
i,
j) * tInternalTensor(
i,
j));
}
Yield function and flow potential
The yield function has form
\[ f(\sigma, \overline{\alpha}) = \sqrt{\frac{3}{2} \eta:\eta} - \overline{\alpha} \]
where
\[ \eta=\textrm{dev}[\sigma]-\overline{\beta} \]
where \(\sigma\) is the stress tensor and \(\overline{\alpha}\) is the scalar internal flux variable, and \(\overline{\beta}\) is tensorial internal flux.
Note that dissipation density can be expressed as
\[ \mathcal{D} = \alpha \overline{\alpha} + \beta : \overline{\beta} \geq 0 \]
The code for which the above function is implemented is given below from ADOLCPlasticityMaterialModels.hpp
auto t_vioght_stress = getFTensor1FromPtr<6>(&a_sTress[0]);
auto t_back_stress = getFTensor1FromPtr<6>(&a_internalFluxes[1]);
tStress(
i,
j) = t_voight_stress_op(
i,
j, Z) * t_vioght_stress(Z);
tBackStress(
i,
j) = t_voight_stress_op(
i,
j, Z) * t_back_stress(Z);
constexpr
double third = boost::math::constants::third<double>();
tDeviator(
i,
j) = tStress(
i,
j) - tR *
t_kd(
i,
j) - tBackStress(
i,
j);
constexpr
double c = 3. / 2.;
f =
c * tDeviator(
i,
j) * tDeviator(
i,
j);
}
a_y = sqrt(
f) - a_internalFluxes[0];
}
Since for J2 plasticity, we assume the associated flow rule, the flow potential is the same as the yield function, i.e. \(\Psi(\sigma, \overline{\alpha}) = f(\sigma, \overline{\alpha})\). In such cases, we can show that the problem could be expressed as a constrained minimization problem of the Lagrangian function
\[ \min_{\alpha, \beta} \max_{\dot{\lambda}} \mathcal{L}(\alpha, \beta,\overline{\alpha}, \overline{\beta}, \dot{\lambda}) := \alpha \overline{\alpha} + \beta : \overline{\beta} + \dot{\gamma} f(\sigma(\varepsilon^e), \overline{\alpha}) \]
where implicit relations between elastic strain and stress, and internal kinematic variables and fluxes are defined by free energy potential. For such cases we dissipation of energy is maximal. If for such a case model prediction matches within reason experiments for curtain range of loading, it indicates that the model captures all fundamental physics of the problem and constitutive equations can not be expressed with a smaller number of parameters that need to be estimated experimentally by independent tests.
- Note
- Any nonassociative flow rule requires additional parameters, and thus the model is less fundamental. For example, if we model granular material such as soil, their dissipation also takes place by friction grains sliding against each other or rotating. The letter part, associated with rotation is not captured by the kinematics of classical continuum description, and many experimental results with nonassociative flow rule are added, with the cost of additional parameters.
J2 plasticity in plane stress
Here we use the classical implementation of finite elements, within displacements as a primary variable, we use the so-called strain-driven approach. For the plane strain case such an approach is natural, and simply emerges from type of use of finite elements, i.e. 2D elements or 3D, and the model presented above remains unchanged.
This is not the case for plane stress, where the constraint that the stress, let's say, in z-direction is zero, needs to be explicitly enforced. That typically leads to some implementation difficulties, i.e. plastic surface is no longer circular, it has an elliptical shape, and a radial return mapping algorithm no longer works. That is a direct result of constraints, which yield a change in the definition of deviatoric stress defined in the 2D word of the plane stress problem.
However, this implementation is straightforward. Since the model is based on potential functions, we choose to implement integration points always in 3D. Specialization between 2D and 3D cases is at the final step while the assembly and construction of finite element base/shape functions, in particular, when the b-bar method is used, to solve the problem of volumetric locking. Note that the plane stress problem is it is not an actual 2D problem, but the reduction of the 3D problem with additional static constrain.
Thus, the implementation of plane stress requires only a change in the definition of free energy, taking into account static constraints, see a snippet from ADOLCPlasticityMaterialModels.hpp
template <> struct J2Plasticity<2> : public J2Plasticity<3> {
using J2Plasticity<3>::J2Plasticity;
auto p_lambda = mkparam(
lambda);
auto p_phi = mkparam(
phi);
auto p_sigma_y = mkparam(
sigmaY);
auto t_voight_total_strain = getFTensor1FromPtr<6>(&a_sTrain[0]);
auto t_voight_plastic_strain = getFTensor1FromPtr<6>(&a_plasticStrain[0]);
auto t_voight_internal_tensor =
getFTensor1FromPtr<6>(&a_internalVariables[1]);
tTotalStrain(
i,
j) = t_voight_strain_op(
i,
j, Z) * t_voight_total_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_plastic_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_internal_tensor(Z);
tElasticStrain(
i,
j) = tTotalStrain(
i,
j) - tPlasticStrain(
i,
j);
tElasticStrain(2, 2) =
(-tElasticStrain(0, 0) * p_lambda - tElasticStrain(1, 1) * p_lambda) /
(p_lambda + 2 * p_mu);
tR = tElasticStrain(
i,
i);
a_w = 0.5 * p_lambda * tR * tR +
p_mu * (tElasticStrain(
i,
j) * tElasticStrain(
i,
j));
a_w +=
a_internalVariables[0] * p_sigma_y +
0.5 * p_phi * p_H * (a_internalVariables[0] * a_internalVariables[0]);
a_w += (0.5 * (1 - p_phi) * p_K) *
(tInternalTensor(
i,
j) * tInternalTensor(
i,
j));
}
};
in particular plane stress constrain is explicitly enforced in the lines
tElasticStrain(2, 2) =
(-tElasticStrain(0, 0) * p_lambda - tElasticStrain(1, 1) * p_lambda) /
(p_lambda + 2 * p_mu);
what is
\[ \varepsilon_{zz} = \frac{-\lambda}{\lambda + 2\mu} \left(\varepsilon_{xx} + \varepsilon_{yy}\right) \]
Paraboloidal model
That is pressure dependent model, which non-associated flow rule. For some applications see papers for reference [71] and [68].
Free energy density
Free energy density has form
\[ \psi = \frac{1}{2} \lambda \textrm{tr}[\varepsilon]^2 + \mu \varepsilon : \varepsilon + \sigma_{yt}\alpha_0 + \frac{1}{2} H_t \alpha_0^2 + \sigma_{yc}\alpha_1 + \frac{1}{2} H_c \alpha_1^2 \]
where \(\lambda\) and \(\mu\) are Lam\'e parameters, \(H_t\) is the hardening modulus in tension, \(H_c\) is the hardening modulus in compression.
The code for which the above function is implemented is given in snippet form ADOLCPlasticityMaterialModels.hpp
auto t_voight_total_strain = getFTensor1FromPtr<6>(&a_sTrain[0]);
auto t_voight_plastic_strain = getFTensor1FromPtr<6>(&a_plasticStrain[0]);
tTotalStrain(
i,
j) = t_voight_strain_op(
i,
j, Z) * t_voight_total_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_plastic_strain(Z);
tElasticStrain(
i,
j) = tTotalStrain(
i,
j) - tPlasticStrain(
i,
j);
tR = tElasticStrain(
i,
i);
a_w = 0.5 *
lambda * tR * tR +
mu * (tElasticStrain(
i,
j) * tElasticStrain(
i,
j));
a_w += sigmaYt * a_internalVariables[0] +
0.5 * Ht * a_internalVariables[0] * a_internalVariables[0];
a_w += sigmaYc * a_internalVariables[1] +
0.5 * Hc * a_internalVariables[1] * a_internalVariables[1];
}
Yield function
The yield function has form
\[ y = 6J_2 + 2I_1\left(\overline{\alpha_1}-\overline{\alpha_0}\right) - 2\overline{\alpha_0} \,\overline{\alpha_1} \]
where the internal fluxes are defined by free energy functional and have from, for compression and tension, respectively, as follows
\[ \overline{\alpha_0}=\frac{\partial \psi}{\partial \alpha_0}=\sigma_{yt} + H_t \alpha_0, \quad \overline{\alpha_1}=\frac{\partial \psi}{\partial \alpha_1}=\sigma_{yc} + H_c \alpha_1 \]
where \(\sigma_{yt}\) is the yield stress in tension, \(\sigma_{yc}\) is the yield stress in compression.
The J2 and I1 stress invariants are defined as follows
\[ I_1 = \textrm{tr} (\boldsymbol{\sigma}), \quad J_2 = \frac{1}{2} \eta:\eta, \]
where \(\eta\) is the deviatoric stress tensor, defined as follows
\[ \eta=\textrm{dev}[\boldsymbol{\sigma}] = \sigma - \frac{1}{3} \textrm{tr} (\boldsymbol{\sigma}) I \]
The implementation of the yield function is given snippet from ADOLCPlasticityMaterialModels.hpp
auto t_vioght_stress = getFTensor1FromPtr<6>(&a_sTress[0]);
tStress(
i,
j) = t_voight_stress_op(
i,
j, Z) * t_vioght_stress(Z);
I1 = tR;
tR /= 3.;
tDeviator(
i,
j) = tStress(
i,
j) - tR *
t_kd(
i,
j);
J2 = 0.5 * (tDeviator(
i,
j) * tDeviator(
i,
j));
}
a_y = 6 * J2 + 2 * I1 * (a_internalFluxes[1] - a_internalFluxes[0]) -
2 * a_internalFluxes[0] * a_internalFluxes[1];
}
Flow potential
The flow potential has form
\[ \Psi = 6J_2 + 2\alpha I_1 \left(\overline{\alpha_1}-\overline{\alpha_0}\right) - 2\overline{\alpha_0} \,\overline{\alpha_1} \]
\[ \alpha= \frac{1-2\nu_p}{1+\nu_p} \]
where \(\nu_p\) is the Poisson ratio of the plastic strain, which for \(\nu_p=0\) model reduces to the associated flow rule, for \(\nu_p=0.5\) the model reduces to the isochoric flow rule. The \(\nu_p\) is an extra material parameter, which has to be tuned to match experimental results. Note that for associated flow rule yield surface and flow potential are parameter-free.
The implementation of the flow potential is given snippet from ADOLCPlasticityMaterialModels.hpp
double alpha =
(1 - 2 * nup) /
(1 + nup);
a_h = 6 * J2 +
2 * alpha * I1 * (a_internalFluxes[1] - a_internalFluxes[0]) -
2 * a_internalFluxes[0] * a_internalFluxes[1];
}
Assembly and integration
The integration of ADOL-C plasticity models with core MoFEM functionality involves three elements, pushing operators for assembly of the right-hand side, i.e. internal forces, and pushing operators to the left-hand side, i.e. tangent matrix. Users can do that using so-called operators factory, which encapsulates all necessary functionality.
The principle behind the operators and operators factory is to create resilient code, that each element of the finite element system is isolated, which interferes with other elements by strictly defined rules. That enforces the modularity of the code. That involves that data are local, and each operator is a kind of black box, which does not depend on the state of other operators. That simplicity of code development, testing, and allows the composition of many components, i.e. different phenomena together.
In the case of plasticity, beyond the assembly linear system of equations, by pushing operators to the left-hand side, and the right-hand side, we need to update history model internal variables, and plastic strains, since elastic-plastic material remembers load history,
Also, the postprocessing of the elastoplastic model requires special attention, while post-processing, since stresses can not be evaluated at post-processing mesh nodes, since the history of deformation is unknown at arbitrary material points, only at integration points used while assembly of the linear system of equations.
As you will see each element, i.e. assembly, updating history, and postprocessing is a black box, the only common data structure is the material model, in which all elements share. This tutorial with little effort can be integrated with ADV-1: Contact problem. Moreover, by evaluating dissipation and assuming that part of it is converted to heat, the user can integrate code with ADV-2: Thermo-elastic example. Another option is coupling with rates of change of the volume, rendering complex physics for hydromechanical problems, i.e. ADV-5: Seepage in elsatic body example.
Note that the tutorial has a general structure that resembles the tasks presented above, see the following code snippet for adolc_plasticity.cpp
Assembly
The pushing of operators to the left-hand side and right-hand side is done by a snippet from adolc_plasticity.cpp
auto add_domain_ops_lhs = [&](auto &pip) {
"GEOMETRY");
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR opFactoryDomainLhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
};
auto add_domain_ops_rhs = [&](auto &pip) {
"GEOMETRY");
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR opFactoryDomainRhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
mField,
"U", pip,
"ADOLCMAT", common_data_ptr,
cpPtr, Sev::inform);
#ifdef ADD_CONTACT
CHKERR ContactOps::opFactoryDomainRhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
pip, "SIGMA", "U");
#endif // ADD_CONTACT
};
CHKERR add_domain_ops_lhs(pipeline_mng->getOpDomainLhsPipeline());
CHKERR add_domain_ops_rhs(pipeline_mng->getOpDomainRhsPipeline());
}
Note "ADOLCMAT" is an arbitrary name of the mesh block, with carrying information about the material model parameters.
Implementation is dimension agnostic, i.e. dimensions of the problem are specialized while code compilation and shape of the elements shape and approximation base orders are decided during the runtimes. However, the implementation of the physics, i.e. elastoplastic phenomena, is free from those considerations about dimensions, order base, or element type.
Have particular attention to ADOLCPlasticity::opFactoryDomainRhs and ADOLCPlasticity::opFactoryDomainLhs, which are directly responsible for pushing operators to the right-hand side and left-hand side, respectively. Those follow patterns that you will find in the other tutorials, i.e. templates specialized for the dimension of the problem, assembly type, integrate method, and operator type. The dimensions of the people are obvious, i.e. 1D, 2D, or 3D.
Assembly could be for example PETSC assembly, that uses simply PETSCc functionality and uses PETSC function MatSetValues. In principle, technically, MatSetValues is specialized in MoFEM, see for example MoFEM::MatSetValues<AssemblyTypeSelector<SCHUR>>. However, users can imagine more complex cases, for example, special assembly for block diagonal parts, i.e. bubbles functions, and prefer calculating Schur complement, see for example VEC-0: Linear elasticity. Other types of assembly are to be written for matrix-free approach, or to GPU. This typically can be separate from the implementation of the physics, i.e. elastoplasticity, that why templatised and specialized if necessary.
Similar considerations are for the integration method, typically GAUSS integrate is used, however, users seeking efficiency can use other methods, i.e. Duffy integrate for fast integration for high-order elements.
Finally, the operator type is responsible for handling abstractions related to specific shapes, dimensions, and element types. We exploit here powerful C++ type checking, to validate that dimension, assembly type, integration method, and operator type are compatible.
Updating history
Setting up the update of history variables is related to the solver you use, i.e. if you would use SNES solver, and program load stepping by yourself, at the end of each step, you need to call a finite element with the right pipeline operators by yourself.
However, in most tutorials, we use PETSC time solver (TS) to carry out time-stepping and inform TS to perform an update of history variables. By doing that we utilize the functionality of PETSC, tested by many users around the world. TS has generic functionality to perform such tasks, i.e. to update history variables, see TSSetPostStep. The only issue is that TSSetPostStep requires passing a pointer to pure "C" function so we have to take care by passing data about the material model
through the same static global variable.
We start with a snippet from adolc_plasticity.cpp, creating time solver
auto ts = pipeline_mng->createTSIM();
double ftime = 1;
CHKERR TSSetMaxTime(ts, ftime);
CHKERR TSSetExactFinalTime(ts, TS_EXACTFINALTIME_MATCHSTEP);
#ifdef ADD_CONTACT
#endif
CHKERR set_section_monitor(ts);
Next, we call function setting TS post-step function,
auto set_up_post_step = [&](auto ts) {
auto create_update_ptr = [&]() {
auto fe_ptr = boost::make_shared<DomainEle>(mField);
fe_ptr->getRuleHook = cpPtr->integrationRule;
{H1});
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
fe_ptr->getOpPtrVector().push_back(
"U", common_data_ptr->getGardAtGaussPtsPtr()));
opFactoryDomainUpdate<SPACE_DIM>(mField, fe_ptr->getOpPtrVector(),
"ADOLCMAT", common_data_ptr, cpPtr),
"push update ops");
return fe_ptr;
};
auto ts_step_post_proc = [](TS ts) {
};
CHKERR TSSetPostStep(ts, ts_step_post_proc);
};
Note that this involves creating finite elements, creating data structures used internally by TS post-step function, and finally registering the function with TS.
Finally, we have to implement the intervention on the elements and execute operators associated with the pipeline. See snippet in ADOLCPlasticity.cpp
struct TSUpdateImpl : public TSUpdate {
TSUpdateImpl(std::string fe_name, boost::shared_ptr<FEMethod> fe_ptr);
private:
boost::shared_ptr<FEMethod> fePtr;
const std::string feName;
};
TSUpdateImpl::TSUpdateImpl(std::string fe_name,
boost::shared_ptr<FEMethod> fe_ptr)
: feName(fe_name), fePtr(fe_ptr) {}
DM dm;
}
boost::shared_ptr<FEMethod> fe_ptr) {
return boost::make_shared<TSUpdateImpl>(fe_name, fe_ptr);
}
You can see again here several levels of code encapsulation, which is necessary for integrating the code with other modules. Note that the user in the future can have other models that also require some update of the state, then it will simply call several update functions inside this snippet in adolc_plasticity.cpp
auto ts_step_post_proc = [](TS ts) {
};
Postprocessing
Postprocessing is a bit more complicated than in the case of linear elasticity. We use Lagrangian formulation, also called material formulation, in which each integration point has an associated material point that does not change through the analysis. For each material point, i.e. integration point, we record history, since the current state, stress, and elastic strain, depend on it.
However, to post-process results, we need to know the current state, such as stress at the mesh nodes, to visualize results in post-processing software, for example Paraview.
To solve that issue we use Discontinuous Galerkin (DG) projection, see implementation in MoFEM::OpLoopThis or see code in dg_projection.cpp. The idea is to build local L2 based on the element, then project the stress and plastic strain on the local base, and then extrapolate to the mesh nodes. DG projection provides general functionality for scalar, vectorial and tensorial quantities, in this tutorial, we use it for stress and plastic strain, which are second-order symmetric tensors. See a snippet from adolc_plasticity.cpp which implements the above idea
auto post_proc_ele_domain = [this](auto &pip_domain, auto &fe_name) {
pip_domain, {
H1,
HDIV},
"GEOMETRY");
auto grad_ptr = boost::make_shared<MatrixDouble>();
pip_domain.push_back(
grad_ptr));
auto op_this = new OpLoopThis<InteriorElem>(mField, fe_name, Sev::noisy);
pip_domain.push_back(op_this);
auto fe_physics = op_this->getThisFEPtr();
auto evaluate_stress_on_physical_element = [&]() {
fe_physics->getRuleHook = cpPtr->integrationRule;
fe_physics->getOpPtrVector(), {H1});
auto common_data_ptr =
boost::make_shared<ADOLCPlasticity::CommonData>();
fe_physics->getOpPtrVector().push_back(
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR cpPtr->addMatBlockOps(mField, fe_physics->getOpPtrVector(),
"ADOLCMAT", Sev::noisy);
fe_physics->getOpPtrVector().push_back(
getRawPtrOpCalculateStress<SPACE_DIM>(mField, common_data_ptr,
cpPtr, false));
return common_data_ptr;
};
auto dg_projection_froward_and_back = [&](auto &common_data_ptr) {
int dg_order = approxOrder - 1;
auto entity_data_l2 =
boost::make_shared<EntitiesFieldData>(MBENTITYSET);
auto mass_ptr =
boost::make_shared<MatrixDouble>();
fe_physics->getOpPtrVector().push_back(new OpDGProjectionMassMatrix(
dg_order, mass_ptr, entity_data_l2, approxBase,
L2));
auto coeffs_ptr_stress = boost::make_shared<MatrixDouble>();
fe_physics->getOpPtrVector().push_back(new OpDGProjectionCoefficients(
common_data_ptr->getStressMatrixPtr(), coeffs_ptr_stress, mass_ptr,
entity_data_l2, approxBase,
L2));
auto coeffs_ptr_plastic_strain = boost::make_shared<MatrixDouble>();
fe_physics->getOpPtrVector().push_back(new OpDGProjectionCoefficients(
common_data_ptr->getPlasticStrainMatrixPtr(),
coeffs_ptr_plastic_strain, mass_ptr, entity_data_l2, approxBase,
pip_domain.push_back(new OpDGProjectionEvaluation(
common_data_ptr->getStressMatrixPtr(), coeffs_ptr_stress,
entity_data_l2, approxBase,
L2));
pip_domain.push_back(new OpDGProjectionEvaluation(
common_data_ptr->getPlasticStrainMatrixPtr(),
coeffs_ptr_plastic_strain, entity_data_l2, approxBase,
L2));
};
auto common_data_ptr = evaluate_stress_on_physical_element();
dg_projection_froward_and_back(common_data_ptr);
return boost::make_tuple(grad_ptr, common_data_ptr->getStressMatrixPtr(),
common_data_ptr->getPlasticStrainMatrixPtr());
};
- Note
- For 3D code implementation have an additional abstraction layer, in which the post-processing element is boundary elements, i.e. face. Then post-processing points at which mesh is evaluated are projected from the face element (boundary) to the volume element (domain), and then the DG projection is run on the domain element. That is part of more general MoFEM functionality, which is used in ADV-1: Contact problem, and in evaluating integrals on mesh skeleton, for methods such as Discontinuous Galerkin, see SCL-11: Discontinuous Galerkin for Poisson problem. The key operator in this case is MoFEM::OpLoopSide.
Example
The best way to run and play with the code is to use the JupyterHub and MoFEM docker container. Follow the instructions in Installation with Docker - JupyterHub Then install the release version for code development, you will find a notebook in the JupterHub folder to do that. If you install the module from scratch, i.e. clone repository, build and install the module, you have to recreate Spack symlink, you simply rerun the last section of the install_from_source_release.md. The outcome of this will be that in folder um_view_release you will find the directory adolc_plasticity, and in it adolc_plasticity.md notebook. Run it and play with the parameters.
You can upload a mesh file and set up the problem in Cubit or gMesh. Also notebook creates zipped VTK files which you can download and post-process in Paraview. Any questions please write to Q&A.
The following figures show the results of the kind of simulation which you can do in Jupyter notebook, see Figure 2 and Figure 3.
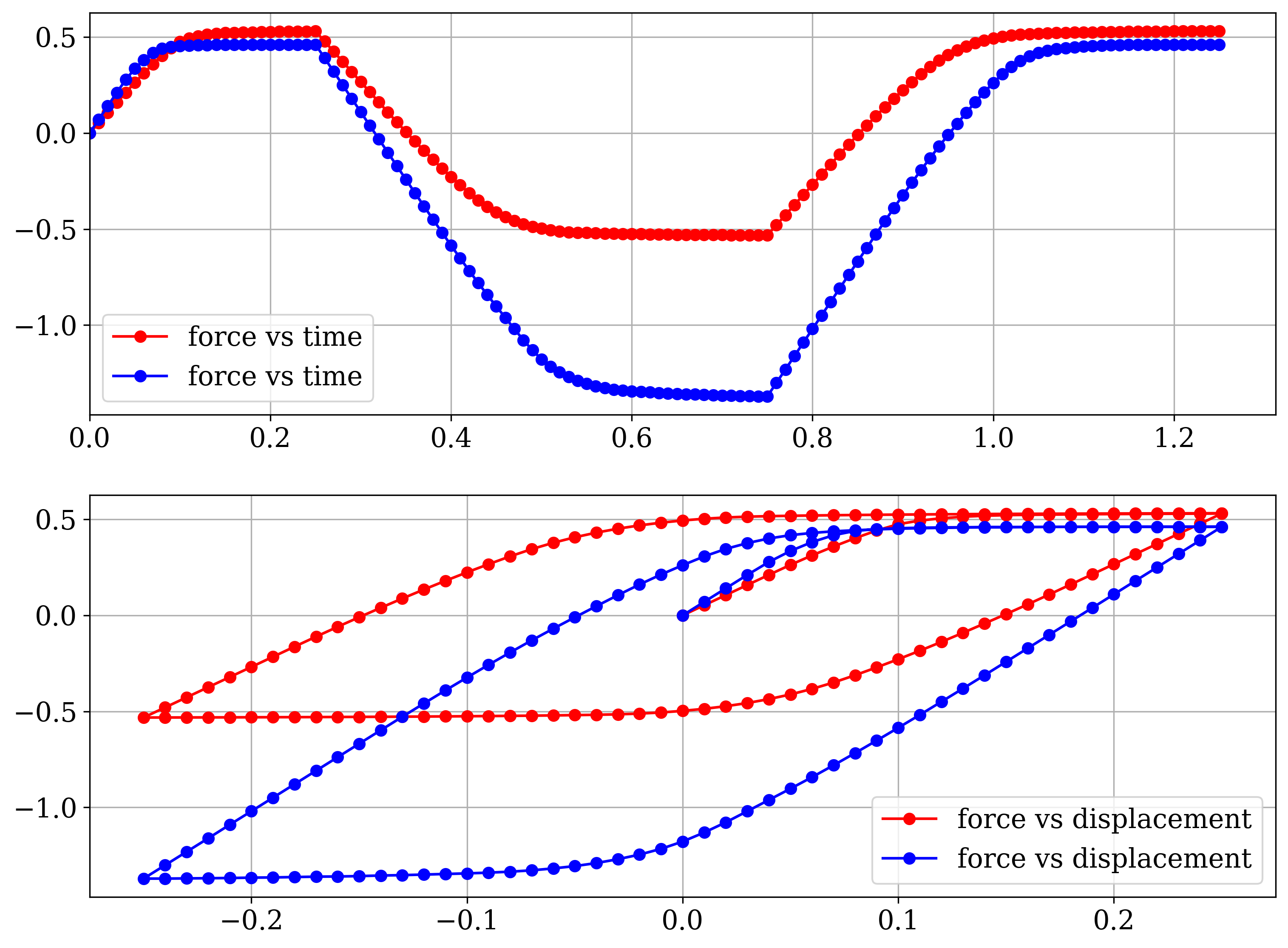
Figure 2: Load history and load vs displacement response for a plate with the hole. Red color is for J2 plasticity response, blue paraboloidal model

Figure 3: On top is the solution for paraboloidal model and on the bottom solution for J2 plasticity.
How to cite?
If you find code, or this tutorial useful, and use it as a guide for your work, please cite the following paper The Journal of Open Source Software
 (follow the link on the badge).
(follow the link on the badge).
Code
template <int DIM>
};
};
#ifdef ADD_CONTACT
#ifdef PYTHON_SDF
#include <boost/python.hpp>
#include <boost/python/def.hpp>
#include <boost/python/numpy.hpp>
namespace bp = boost::python;
namespace np = boost::python::numpy;
#endif
};
#endif // ADD_CONTACT
private:
int approxOrder = 2;
boost::shared_ptr<ClosestPointProjection> cpPtr;
#ifdef ADD_CONTACT
#ifdef PYTHON_SDF
boost::shared_ptr<ContactOps::SDFPython> sdfPythonPtr;
#endif
#endif // ADD_CONTACT
};
}
}
enum bases { AINSWORTH, DEMKOWICZ, LASBASETOPT };
const char *list_bases[LASBASETOPT] = {"ainsworth", "demkowicz"};
PetscInt choice_base_value = AINSWORTH;
LASBASETOPT, &choice_base_value, PETSC_NULL);
PETSC_NULL);
switch (choice_base_value) {
case AINSWORTH:
<< "Set AINSWORTH_LEGENDRE_BASE for displacements";
break;
case DEMKOWICZ:
<< "Set DEMKOWICZ_JACOBI_BASE for displacements";
break;
default:
break;
}
#ifdef ADD_CONTACT
CHKERR skin.find_skin(0, body_ents,
false, skin_ents);
return skin_ents;
};
auto filter_blocks = [&](auto skin) {
bool is_contact_block = false;
(boost::format("%s(.*)") % "CONTACT").str()
))
) {
is_contact_block =
true;
<<
"Find contact block set: " <<
m->getName();
auto meshset =
m->getMeshset();
Range contact_meshset_range;
meshset,
SPACE_DIM - 1, contact_meshset_range,
true);
contact_meshset_range);
contact_range.merge(contact_meshset_range);
}
if (is_contact_block) {
<< "Nb entities in contact surface: " << contact_range.size();
skin = intersect(skin, contact_range);
}
return skin;
};
ParallelComm *pcomm =
CHKERR pcomm->filter_pstatus(skin, PSTATUS_SHARED | PSTATUS_MULTISHARED,
PSTATUS_NOT, -1, &boundary_ents);
return boundary_ents;
};
#ifdef ADD_CONTACT
CHKERR simple->setFieldOrder(
"SIGMA", approxOrder - 1, &boundary_ents);
#endif
#ifdef PYTHON_SDF
sdfPythonPtr = boost::make_shared<ContactOps::SDFPython>();
CHKERR sdfPythonPtr->sdfInit(
"sdf.py");
ContactOps::sdfPythonWeakPtr = sdfPythonPtr;
#endif
#endif
auto project_ho_geometry = [&]() {
return mField.
loop_dofs(
"GEOMETRY", ent_method);
};
PetscBool project_geometry = PETSC_TRUE;
&project_geometry, PETSC_NULL);
if (project_geometry) {
}
enum MaterialModel {
VonMisses,
VonMissesPlaneStress,
Paraboloidal,
LastModel
};
const char *list_materials[LastModel] = {"VonMisses", "VonMissesPlaneStress",
"Paraboloidal"};
PetscInt choice_material = VonMisses;
LastModel, &choice_material, PETSC_NULL);
switch (choice_material) {
case VonMisses:
cpPtr = createMaterial<J2Plasticity<3>>();
break;
case VonMissesPlaneStress:
"VonMissesPlaneStrain is only for 2D case");
cpPtr = createMaterial<J2Plasticity<2>>();
break;
case Paraboloidal:
cpPtr = createMaterial<ParaboloidalPlasticity>();
break;
default:
}
cpPtr->integrationRule = [](
int,
int,
int p) {
return 2 * (p - 2); };
}
auto time_scale = boost::make_shared<TimeScale>();
auto rule = [](
int,
int,
int p) {
return 2 * p; };
CHKERR pipeline_mng->setDomainRhsIntegrationRule(cpPtr->integrationRule);
CHKERR pipeline_mng->setDomainLhsIntegrationRule(cpPtr->integrationRule);
CHKERR pipeline_mng->setBoundaryRhsIntegrationRule(rule);
CHKERR pipeline_mng->setBoundaryLhsIntegrationRule(rule);
pipeline_mng->getOpBoundaryLhsPipeline(), {HDIV}, "GEOMETRY");
pipeline_mng->getOpBoundaryLhsPipeline().push_back(
pipeline_mng->getOpBoundaryRhsPipeline(), {HDIV}, "GEOMETRY");
pipeline_mng->getOpBoundaryRhsPipeline().push_back(
pipeline_mng->getOpBoundaryRhsPipeline(), mField, "U", {time_scale},
Sev::inform);
pipeline_mng->getOpBoundaryLhsPipeline(), mField, "U", Sev::inform);
#ifdef ADD_CONTACT
ContactOps::opFactoryBoundaryLhs<SPACE_DIM, PETSC, GAUSS, BoundaryEleOp>(
pipeline_mng->getOpBoundaryLhsPipeline(), "SIGMA", "U");
ContactOps::opFactoryBoundaryToDomainLhs<SPACE_DIM, PETSC, GAUSS, DomainEle>(
mField, pipeline_mng->getOpBoundaryLhsPipeline(),
simple->getDomainFEName(),
"SIGMA",
"U",
"GEOMETRY",
cpPtr->integrationRule);
ContactOps::opFactoryBoundaryRhs<SPACE_DIM, PETSC, GAUSS, BoundaryEleOp>(
pipeline_mng->getOpBoundaryRhsPipeline(), "SIGMA", "U");
#endif // ADD_CONTACT
pipeline_mng->getOpDomainRhsPipeline(), mField, "U", {time_scale},
"BODY_FORCE", Sev::inform);
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(),
"REMOVE_X",
"U", 0, 0);
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(),
"REMOVE_Y",
"U", 1, 1);
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(),
"REMOVE_Z",
"U", 2, 2);
#ifdef ADD_CONTACT
for (auto b : {"FIX_X", "REMOVE_X"})
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(), b,
"SIGMA", 0, 0, false, true);
for (auto b : {"FIX_Y", "REMOVE_Y"})
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(), b,
"SIGMA", 1, 1, false, true);
for (auto b : {"FIX_Z", "REMOVE_Z"})
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(), b,
"SIGMA", 2, 2, false, true);
for (auto b : {"FIX_ALL", "REMOVE_ALL"})
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(), b,
"SIGMA", 0, 3, false, true);
CHKERR bc_mng->removeBlockDOFsOnEntities(
simple->getProblemName(),
"NO_CONTACT",
"SIGMA", 0, 3,
false,
true);
#endif
simple->getProblemName(),
"U");
}
auto add_domain_ops_lhs = [&](auto &pip) {
"GEOMETRY");
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR opFactoryDomainLhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
mField, "U", pip, "ADOLCMAT", common_data_ptr, cpPtr);
};
auto add_domain_ops_rhs = [&](auto &pip) {
"GEOMETRY");
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR opFactoryDomainRhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
mField, "U", pip, "ADOLCMAT", common_data_ptr, cpPtr, Sev::inform);
#ifdef ADD_CONTACT
CHKERR ContactOps::opFactoryDomainRhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
pip, "SIGMA", "U");
#endif // ADD_CONTACT
};
CHKERR add_domain_ops_lhs(pipeline_mng->getOpDomainLhsPipeline());
CHKERR add_domain_ops_rhs(pipeline_mng->getOpDomainRhsPipeline());
}
std::pair<boost::shared_ptr<PostProcEleDomain>,
boost::shared_ptr<PostProcEleBdy>>
pair_post_proc_fe,
boost::shared_ptr<DomainEle> reaction_fe,
std::vector<boost::shared_ptr<ScalingMethod>> smv)
: dM(dm), reactionFE(reaction_fe), vecOfTimeScalingMethods(smv) {
domainPostProcFe = pair_post_proc_fe.first;
skinPostProcFe = pair_post_proc_fe.second;
#ifdef ADD_CONTACT
auto get_integrate_traction = [&]() {
auto integrate_traction = boost::make_shared<BoundaryEle>(*m_field_ptr);
auto common_data_ptr = boost::make_shared<ContactOps::CommonData>();
integrate_traction->getOpPtrVector(), {HDIV}, "GEOMETRY")),
"Apply transform");
integrate_traction->getOpPtrVector().push_back(
};
integrate_traction->getOpPtrVector(), "SIGMA", 0)),
"push operators to calculate traction");
return integrate_traction;
};
integrateTraction = get_integrate_traction();
#endif
}
#ifdef ADD_CONTACT
auto print_traction = [&](const std::string msg) {
const double *t_ptr;
MOFEM_LOG_C(
"CONTACT", Sev::inform,
"%s time %3.4e %3.4e %3.4e %3.4e",
msg.c_str(), ts_t, t_ptr[0], t_ptr[1], t_ptr[2]);
&t_ptr);
}
};
#endif
auto make_vtk = [&]() {
if (domainPostProcFe) {
getCacheWeakPtr());
CHKERR domainPostProcFe->writeFile(
"out_plastic_" + boost::lexical_cast<std::string>(ts_step) +
".h5m");
}
if (skinPostProcFe) {
getCacheWeakPtr());
CHKERR skinPostProcFe->writeFile(
"out_skin_plastic_" + boost::lexical_cast<std::string>(ts_step) +
".h5m");
}
};
}
if (reactionFE) {
reactionFE->f = fRes;
CHKERR VecAssemblyBegin(fRes);
CHKERR VecGhostUpdateBegin(fRes, ADD_VALUES, SCATTER_REVERSE);
CHKERR VecGhostUpdateEnd(fRes, ADD_VALUES, SCATTER_REVERSE);
*m_field_ptr, reactionFE, fRes)();
double nrm;
CHKERR VecNorm(fRes, NORM_2, &nrm);
<< "Residual norm " << nrm << " at time step " << ts_step;
}
#ifdef ADD_CONTACT
auto calculate_traction = [&] {
};
#endif
auto get_min_max_displacement = [&]() {
std::array<double, 4> a_min = {DBL_MAX, DBL_MAX, DBL_MAX, 0};
std::array<double, 4> a_max = {-DBL_MAX, -DBL_MAX, -DBL_MAX, 0};
auto get_min_max = [&](boost::shared_ptr<FieldEntity> field_entity_ptr) {
for (
auto v : field_entity_ptr->getEntFieldData()) {
a_min[
d] = std::min(a_min[
d],
v);
a_max[
d] = std::max(a_max[
d],
v);
}
};
get_min_max, "U", &verts);
auto mpi_reduce = [&](
auto &
a,
auto op) {
std::array<double, 3> a_mpi = {0, 0, 0};
MPI_Allreduce(
a.data(), a_mpi.data(), 3, MPI_DOUBLE, op,
return a_mpi;
};
auto a_min_mpi = mpi_reduce(a_min, MPI_MIN);
auto a_max_mpi = mpi_reduce(a_max, MPI_MAX);
<< "Min displacement " << a_min_mpi[0] << " " << a_min_mpi[1] << " "
<< a_min_mpi[2];
<< "Max displacement " << a_max_mpi[0] << " " << a_max_mpi[1] << " "
<< a_max_mpi[2];
};
CHKERR get_min_max_displacement();
#ifdef ADD_CONTACT
CHKERR print_traction(
"Contact force");
#endif
for (auto s : vecOfTimeScalingMethods) {
scale *= s->getScale(this->ts_t);
}
<<
"Time: " << this->ts_t <<
" scale: " <<
scale;
}
private:
boost::shared_ptr<PostProcEleDomain> domainPostProcFe;
boost::shared_ptr<PostProcEleBdy> skinPostProcFe;
boost::shared_ptr<FEMethod> reactionFE;
boost::shared_ptr<BoundaryEle> integrateTraction;
};
auto time_scale = boost::make_shared<TimeScale>();
auto create_post_proc_fe = [dm,
this,
simple]() {
auto post_proc_ele_domain = [this](auto &pip_domain, auto &fe_name) {
pip_domain, {
H1,
HDIV},
"GEOMETRY");
auto grad_ptr = boost::make_shared<MatrixDouble>();
pip_domain.push_back(
grad_ptr));
pip_domain.push_back(op_this);
auto fe_physics = op_this->getThisFEPtr();
auto evaluate_stress_on_physical_element = [&]() {
fe_physics->getRuleHook = cpPtr->integrationRule;
fe_physics->getOpPtrVector(), {H1});
auto common_data_ptr =
boost::make_shared<ADOLCPlasticity::CommonData>();
fe_physics->getOpPtrVector().push_back(
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR cpPtr->addMatBlockOps(mField, fe_physics->getOpPtrVector(),
"ADOLCMAT", Sev::noisy);
fe_physics->getOpPtrVector().push_back(
getRawPtrOpCalculateStress<SPACE_DIM>(mField, common_data_ptr,
cpPtr, false));
return common_data_ptr;
};
auto dg_projection_froward_and_back = [&](auto &common_data_ptr) {
int dg_order = approxOrder - 1;
auto entity_data_l2 =
boost::make_shared<EntitiesFieldData>(MBENTITYSET);
auto mass_ptr =
boost::make_shared<MatrixDouble>();
dg_order, mass_ptr, entity_data_l2, approxBase,
L2));
auto coeffs_ptr_stress = boost::make_shared<MatrixDouble>();
common_data_ptr->getStressMatrixPtr(), coeffs_ptr_stress, mass_ptr,
entity_data_l2, approxBase,
L2));
auto coeffs_ptr_plastic_strain = boost::make_shared<MatrixDouble>();
common_data_ptr->getPlasticStrainMatrixPtr(),
coeffs_ptr_plastic_strain, mass_ptr, entity_data_l2, approxBase,
common_data_ptr->getStressMatrixPtr(), coeffs_ptr_stress,
entity_data_l2, approxBase,
L2));
common_data_ptr->getPlasticStrainMatrixPtr(),
coeffs_ptr_plastic_strain, entity_data_l2, approxBase,
L2));
};
auto common_data_ptr = evaluate_stress_on_physical_element();
dg_projection_froward_and_back(common_data_ptr);
return boost::make_tuple(grad_ptr, common_data_ptr->getStressMatrixPtr(),
common_data_ptr->getPlasticStrainMatrixPtr());
};
auto add_post_proc_map = [&](auto post_proc_fe, auto u_ptr, auto grad_ptr,
auto stress_ptr, auto plastic_strain_ptr,
auto contact_stress_ptr, auto X_ptr) {
post_proc_fe->getOpPtrVector().push_back(
new OpPPMapSPACE_DIM(
post_proc_fe->getPostProcMesh(), post_proc_fe->getMapGaussPts(),
{},
{{"U", u_ptr}, {"GEOMETRY", X_ptr}},
{{"GRAD", grad_ptr}, {"SIGMA", contact_stress_ptr}},
{}
)
);
post_proc_fe->getOpPtrVector().push_back(
new OpPPMap3D(
post_proc_fe->getPostProcMesh(), post_proc_fe->getMapGaussPts(),
{},
{},
{},
{{"STRESS", stress_ptr}, {"PLASTIC_STRAIN", plastic_strain_ptr}}
)
);
return post_proc_fe;
};
auto vol_post_proc = [
this,
simple, post_proc_ele_domain,
add_post_proc_map]() {
PetscBool post_proc_vol = PETSC_FALSE;
post_proc_vol = PETSC_TRUE;
&post_proc_vol, PETSC_NULL);
if (post_proc_vol == PETSC_FALSE)
return boost::shared_ptr<PostProcEleDomain>();
auto post_proc_fe = boost::make_shared<PostProcEleDomain>(mField);
auto u_ptr = boost::make_shared<MatrixDouble>();
post_proc_fe->getOpPtrVector().push_back(
auto X_ptr = boost::make_shared<MatrixDouble>();
post_proc_fe->getOpPtrVector().push_back(
auto contact_stress_ptr = boost::make_shared<MatrixDouble>();
#ifdef ADD_CONTACT
post_proc_fe->getOpPtrVector().push_back(
"SIGMA", contact_stress_ptr));
#else
contact_stress_ptr = nullptr;
#endif
auto [grad_ptr, stress_ptr, plastic_strain_ptr] = post_proc_ele_domain(
post_proc_fe->getOpPtrVector(),
simple->getDomainFEName());
return add_post_proc_map(post_proc_fe, u_ptr, grad_ptr, stress_ptr,
plastic_strain_ptr, contact_stress_ptr, X_ptr);
};
auto skin_post_proc = [
this,
simple, post_proc_ele_domain,
add_post_proc_map]() {
PetscBool post_proc_skin = PETSC_TRUE;
post_proc_skin = PETSC_FALSE;
&post_proc_skin, PETSC_NULL);
if (post_proc_skin == PETSC_FALSE)
return boost::shared_ptr<PostProcEleBdy>();
auto post_proc_fe = boost::make_shared<PostProcEleBdy>(mField);
auto u_ptr = boost::make_shared<MatrixDouble>();
post_proc_fe->getOpPtrVector().push_back(
auto X_ptr = boost::make_shared<MatrixDouble>();
post_proc_fe->getOpPtrVector().push_back(
auto contact_stress_ptr = boost::make_shared<MatrixDouble>();
auto op_loop_side =
auto [grad_ptr, stress_ptr, plastic_strain_ptr] = post_proc_ele_domain(
op_loop_side->getOpPtrVector(),
simple->getDomainFEName());
#ifdef ADD_CONTACT
op_loop_side->getOpPtrVector().push_back(
"SIGMA", contact_stress_ptr));
#else
contact_stress_ptr = nullptr;
#endif
post_proc_fe->getOpPtrVector().push_back(op_loop_side);
return add_post_proc_map(post_proc_fe, u_ptr, grad_ptr, stress_ptr,
plastic_strain_ptr, contact_stress_ptr, X_ptr);
};
return std::make_pair(vol_post_proc(), skin_post_proc());
};
auto create_reaction_fe = [&]() {
auto fe_ptr = boost::make_shared<DomainEle>(mField);
fe_ptr->getRuleHook = cpPtr->integrationRule;
auto &pip = fe_ptr->getOpPtrVector();
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
"U", common_data_ptr->getGardAtGaussPtsPtr()));
CHKERR opFactoryDomainRhs<SPACE_DIM, PETSC, GAUSS, DomainEleOp>(
mField, "U", pip, "ADOLCMAT", common_data_ptr, cpPtr, Sev::noisy);
return fe_ptr;
};
auto add_extra_finite_elements_to_ksp_solver_pipelines = [&]() {
auto pre_proc_ptr = boost::make_shared<FEMethod>();
auto post_proc_rhs_ptr = boost::make_shared<FEMethod>();
auto post_proc_lhs_ptr = boost::make_shared<FEMethod>();
auto get_bc_hook_rhs = [this, pre_proc_ptr, time_scale]() {
{time_scale}, false)();
};
pre_proc_ptr->preProcessHook = get_bc_hook_rhs;
auto get_post_proc_hook_rhs = [this, post_proc_rhs_ptr]() {
mField, post_proc_rhs_ptr, nullptr, Sev::verbose)();
mField, post_proc_rhs_ptr, 1.)();
};
auto get_post_proc_hook_lhs = [this, post_proc_lhs_ptr]() {
mField, post_proc_lhs_ptr, 1.)();
};
post_proc_rhs_ptr->postProcessHook = get_post_proc_hook_rhs;
post_proc_lhs_ptr->postProcessHook = get_post_proc_hook_lhs;
ts_ctx_ptr->getPreProcessIFunction().push_front(pre_proc_ptr);
ts_ctx_ptr->getPreProcessIJacobian().push_front(pre_proc_ptr);
ts_ctx_ptr->getPostProcessIFunction().push_back(post_proc_rhs_ptr);
ts_ctx_ptr->getPostProcessIJacobian().push_back(post_proc_lhs_ptr);
};
CHKERR add_extra_finite_elements_to_ksp_solver_pipelines();
auto create_monitor_fe = [dm, time_scale](auto &&post_proc_fe,
auto &&reaction_fe) {
return boost::make_shared<Monitor>(
dm, post_proc_fe, reaction_fe,
std::vector<boost::shared_ptr<ScalingMethod>>{time_scale});
};
auto set_up_post_step = [&](auto ts) {
auto create_update_ptr = [&]() {
auto fe_ptr = boost::make_shared<DomainEle>(mField);
fe_ptr->getRuleHook = cpPtr->integrationRule;
{H1});
auto common_data_ptr = boost::make_shared<ADOLCPlasticity::CommonData>();
fe_ptr->getOpPtrVector().push_back(
"U", common_data_ptr->getGardAtGaussPtsPtr()));
opFactoryDomainUpdate<SPACE_DIM>(mField, fe_ptr->getOpPtrVector(),
"ADOLCMAT", common_data_ptr, cpPtr),
"push update ops");
return fe_ptr;
};
auto ts_step_post_proc = [](TS ts) {
};
CHKERR TSSetPostStep(ts, ts_step_post_proc);
};
auto set_up_monitor = [&](auto ts) {
boost::shared_ptr<FEMethod> null_fe;
auto monitor_ptr =
create_monitor_fe(create_post_proc_fe(), create_reaction_fe());
null_fe, monitor_ptr);
};
auto set_section_monitor = [&](auto solver) {
SNES snes;
CHKERR TSGetSNES(solver, &snes);
(void *)(snes_ctx_ptr.get()), nullptr);
};
auto set_up_adapt = [&](auto ts) {
TSAdapt adapt;
CHKERR TSGetAdapt(ts, &adapt);
};
auto ts = pipeline_mng->createTSIM();
double ftime = 1;
CHKERR TSSetMaxTime(ts, ftime);
CHKERR TSSetExactFinalTime(ts, TS_EXACTFINALTIME_MATCHSTEP);
#ifdef ADD_CONTACT
#endif
CHKERR set_section_monitor(ts);
PetscInt steps, snesfails, rejects, nonlinits, linits;
CHKERR TSGetStepNumber(ts, &steps);
CHKERR TSGetSNESFailures(ts, &snesfails);
CHKERR TSGetStepRejections(ts, &rejects);
CHKERR TSGetSNESIterations(ts, &nonlinits);
CHKERR TSGetKSPIterations(ts, &linits);
"steps %d (%d rejected, %d SNES fails), ftime %g, nonlinits "
"%d, linits %d",
steps, rejects, snesfails, ftime, nonlinits, linits);
}
SCATTER_FORWARD);
double nrm2;
CHKERR VecNorm(T, NORM_2, &nrm2);
MOFEM_LOG(
"PlasticPrb", Sev::inform) <<
"Solution norm " << nrm2;
auto post_proc_norm_fe = boost::make_shared<DomainEle>(
mField);
post_proc_norm_fe->getRuleHook =
cpPtr->integrationRule;
post_proc_norm_fe->getOpPtrVector(), {H1});
enum NORMS { U_NORM_L2 = 0, PIOLA_NORM, LAST_NORM };
auto norms_vec =
CHKERR VecZeroEntries(norms_vec);
auto u_ptr = boost::make_shared<MatrixDouble>();
post_proc_norm_fe->getOpPtrVector().push_back(
post_proc_norm_fe->getOpPtrVector().push_back(
post_proc_norm_fe);
CHKERR VecAssemblyBegin(norms_vec);
CHKERR VecAssemblyEnd(norms_vec);
const double *norms;
CHKERR VecGetArrayRead(norms_vec, &norms);
<< "norm_u: " << std::scientific << std::sqrt(norms[U_NORM_L2]);
CHKERR VecRestoreArrayRead(norms_vec, &norms);
}
}
PetscInt test_nb = 0;
PetscBool test_flg = PETSC_FALSE;
if (test_flg) {
SCATTER_FORWARD);
double nrm2;
CHKERR VecNorm(T, NORM_2, &nrm2);
MOFEM_LOG(
"PlasticPrb", Sev::verbose) <<
"Regression norm " << nrm2;
double regression_value = 0;
switch (test_nb) {
default:
break;
}
if (fabs(nrm2 - regression_value) > 1e-2)
"Regression test field; wrong norm value. %6.4e != %6.4e", nrm2,
regression_value);
}
}
#ifdef ADD_CONTACT
#endif
}
static char help[] =
"...\n\n";
int main(
int argc,
char *argv[]) {
#ifdef ADD_CONTACT
#ifdef PYTHON_SDF
Py_Initialize();
np::initialize();
#endif
#endif // ADD_CONTACT
const char param_file[] = "param_file.petsc";
auto core_log = logging::core::get();
core_log->add_sink(
LogManager::createSink(LogManager::getStrmWorld(), "PlasticPrb"));
LogManager::setLog("PlasticPrb");
#ifdef ADD_CONTACT
core_log->add_sink(
LogManager::createSink(LogManager::getStrmWorld(), "CONTACT"));
LogManager::setLog("CONTACT");
#endif // ADD_CONTACT
try {
DMType dm_name = "DMMOFEM";
}
#ifdef ADD_CONTACT
#ifdef PYTHON_SDF
if (Py_FinalizeEx() < 0) {
exit(120);
}
#endif
#endif // ADD_CONTACT
return 0;
}
#ifndef __ADOLC_MATERIAL_MODELS_HPP
#define __ADOLC_MATERIAL_MODELS_HPP
#ifndef WITH_ADOL_C
#error "MoFEM need to be compiled with ADOL-C"
#endif
template <int DIM> struct J2Plasticity;
template <> struct J2Plasticity<3> : public ClosestPointProjection {
J2Plasticity() : ClosestPointProjection() {
nbInternalVariables = 7;
activeVariablesW.resize(12 + nbInternalVariables, false);
}
enum ModelParams {
LAMBDA,
MU, ISOH, KINK, PHI, SIGMA_Y, LAST_PARAM };
using ParamsArray = std::array<double, LAST_PARAM>;
boost::shared_ptr<ParamsArray> defaultParamsArrayPtr = nullptr;
boost::shared_ptr<ParamsArray> paramsArrayPtr = nullptr;
boost::shared_ptr<ParamsArray> oldParamsArrayPtr = nullptr;
PETSC_NULL);
0);
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
defaultParamsArrayPtr = boost::make_shared<ParamsArray>();
(*defaultParamsArrayPtr)[
MU] =
mu;
(*defaultParamsArrayPtr)[
H] =
H;
(*defaultParamsArrayPtr)[
K] =
K;
(*defaultParamsArrayPtr)[PHI] =
phi;
(*defaultParamsArrayPtr)[SIGMA_Y] =
sigmaY;
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"LAMBDA: " << (*defaultParamsArrayPtr)[
LAMBDA];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"MU: " << (*defaultParamsArrayPtr)[
MU];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<< "H: " << (*defaultParamsArrayPtr)[ISOH];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<< "K: " << (*defaultParamsArrayPtr)[KINK];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<< "PHI: " << (*defaultParamsArrayPtr)[PHI];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<< "SIGMA_Y: " << (*defaultParamsArrayPtr)[SIGMA_Y];
paramsArrayPtr = boost::make_shared<ParamsArray>();
std::copy(defaultParamsArrayPtr->begin(), defaultParamsArrayPtr->end(),
paramsArrayPtr->begin());
oldParamsArrayPtr = boost::make_shared<ParamsArray>();
std::fill(oldParamsArrayPtr->begin(), oldParamsArrayPtr->end(), 0);
};
boost::ptr_deque<ForcesAndSourcesCore::UserDataOperator> &pip,
std::string block_name,
Sev sev) {
OpMatBlocks(boost::shared_ptr<ParamsArray> params_array_ptr,
boost::shared_ptr<ParamsArray> def_params_array_otr,
std::vector<const CubitMeshSets *> meshset_vec_ptr)
:
OP(
NOSPACE,
OP::OPSPACE), paramsArrayPtr(params_array_ptr),
defParamsArray(def_params_array_otr) {
"Can not get data from block");
}
for (auto &b : blockData) {
if (b.blockEnts.find(getFEEntityHandle()) != b.blockEnts.end()) {
std::copy(b.paramsArray.begin(), b.paramsArray.end(),
paramsArrayPtr->begin());
}
}
std::copy(defParamsArray->begin(), defParamsArray->end(),
paramsArrayPtr->begin());
}
private:
boost::shared_ptr<ParamsArray> paramsArrayPtr;
boost::shared_ptr<ParamsArray> defParamsArray;
ParamsArray paramsArray;
};
std::vector<BlockData> blockData;
std::vector<const CubitMeshSets *> meshset_vec_ptr,
for (
auto m : meshset_vec_ptr) {
std::vector<double> block_data;
CHKERR m->getAttributes(block_data);
if (block_data.size() != 6) {
"Expected that block has two attribute");
}
auto get_block_ents = [&]() {
m_field.
get_moab().get_entities_by_handle(
m->meshset, ents,
true);
return ents;
};
blockData.push_back({*defParamsArray, get_block_ents()});
std::copy(block_data.begin(), block_data.end(),
blockData.back().paramsArray.begin());
<<
"Young modulus: " << (blockData.back().paramsArray)[
LAMBDA];
<<
"Poisson ratio: " << (blockData.back().paramsArray)[
MU];
blockData.back().paramsArray[
LAMBDA] =
<<
"LAMBDA: " << (blockData.back().paramsArray)[
LAMBDA];
<<
"MU: " << (blockData.back().paramsArray)[
MU];
<< "H: " << (blockData.back().paramsArray)[ISOH];
<< "K: " << (blockData.back().paramsArray)[KINK];
<< "PHI: " << (blockData.back().paramsArray)[PHI];
<< "SIGMA_Y: " << (blockData.back().paramsArray)[SIGMA_Y];
}
}
};
auto cubit_meshsets_vec_ptr =
m_field.
getInterface<MeshsetsManager>()->getCubitMeshsetPtr(
std::regex((boost::format("%s(.*)") % block_name).str()));
pip.push_back(new OpMatBlocks(paramsArrayPtr, defaultParamsArrayPtr,
m_field, sev, cubit_meshsets_vec_ptr));
}
MoFEMErrorCode setParams(
short tag,
bool &recalculate_elastic_tangent) {
switch (tag) {
set_param_vec(tapesTags[tag], paramsArrayPtr->size(),
paramsArrayPtr->data());
for (auto p = 0; p != LAST_PARAM; p++) {
if ((*paramsArrayPtr)[p] != (*oldParamsArrayPtr)[p]) {
recalculate_elastic_tangent = true;
std::copy(paramsArrayPtr->begin(), paramsArrayPtr->end(),
oldParamsArrayPtr->begin());
break;
}
}
} break;
case TypesTags::Y:
break;
default:
"Unknown tag for setParams");
}
}
auto p_lambda = mkparam(
lambda);
auto p_phi = mkparam(
phi);
auto p_sigma_y = mkparam(
sigmaY);
auto t_voight_total_strain = getFTensor1FromPtr<6>(&a_sTrain[0]);
auto t_voight_plastic_strain = getFTensor1FromPtr<6>(&a_plasticStrain[0]);
auto t_voight_internal_tensor =
getFTensor1FromPtr<6>(&a_internalVariables[1]);
tTotalStrain(
i,
j) = t_voight_strain_op(
i,
j, Z) * t_voight_total_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_plastic_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_internal_tensor(Z);
tElasticStrain(
i,
j) = tTotalStrain(
i,
j) - tPlasticStrain(
i,
j);
tR = tElasticStrain(
i,
i);
a_w = 0.5 * p_lambda * tR * tR +
p_mu * (tElasticStrain(
i,
j) * tElasticStrain(
i,
j));
a_w +=
a_internalVariables[0] * p_sigma_y +
0.5 * p_phi * p_H * (a_internalVariables[0] * a_internalVariables[0]);
a_w += (0.5 * (1 - p_phi) * p_K) *
(tInternalTensor(
i,
j) * tInternalTensor(
i,
j));
}
auto t_vioght_stress = getFTensor1FromPtr<6>(&a_sTress[0]);
auto t_back_stress = getFTensor1FromPtr<6>(&a_internalFluxes[1]);
tStress(
i,
j) = t_voight_stress_op(
i,
j, Z) * t_vioght_stress(Z);
tBackStress(
i,
j) = t_voight_stress_op(
i,
j, Z) * t_back_stress(Z);
constexpr
double third = boost::math::constants::third<double>();
tDeviator(
i,
j) = tStress(
i,
j) - tR *
t_kd(
i,
j) - tBackStress(
i,
j);
constexpr
double c = 3. / 2.;
f =
c * tDeviator(
i,
j) * tDeviator(
i,
j);
}
a_y = sqrt(
f) - a_internalFluxes[0];
}
a_h = sqrt(
f) - a_internalFluxes[0];
}
};
template <> struct J2Plasticity<2> : public J2Plasticity<3> {
auto p_lambda = mkparam(
lambda);
auto p_phi = mkparam(
phi);
auto p_sigma_y = mkparam(
sigmaY);
auto t_voight_total_strain = getFTensor1FromPtr<6>(&a_sTrain[0]);
auto t_voight_plastic_strain = getFTensor1FromPtr<6>(&a_plasticStrain[0]);
auto t_voight_internal_tensor =
getFTensor1FromPtr<6>(&a_internalVariables[1]);
tTotalStrain(
i,
j) = t_voight_strain_op(
i,
j, Z) * t_voight_total_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_plastic_strain(Z);
t_voight_strain_op(
i,
j, Z) * t_voight_internal_tensor(Z);
tElasticStrain(
i,
j) = tTotalStrain(
i,
j) - tPlasticStrain(
i,
j);
tElasticStrain(2, 2) =
(-tElasticStrain(0, 0) * p_lambda - tElasticStrain(1, 1) * p_lambda) /
(p_lambda + 2 * p_mu);
tR = tElasticStrain(
i,
i);
a_w = 0.5 * p_lambda * tR * tR +
p_mu * (tElasticStrain(
i,
j) * tElasticStrain(
i,
j));
a_w +=
a_internalVariables[0] * p_sigma_y +
0.5 * p_phi * p_H * (a_internalVariables[0] * a_internalVariables[0]);
a_w += (0.5 * (1 - p_phi) * p_K) *
(tInternalTensor(
i,
j) * tInternalTensor(
i,
j));
}
};
struct ParaboloidalPlasticity : public ClosestPointProjection {
}
};
PETSC_NULL);
0);
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
(*defaultParamsArrayPtr)[
MU] =
mu;
(*defaultParamsArrayPtr)[
NUP] =
nup;
(*defaultParamsArrayPtr)[
HT] =
Ht;
(*defaultParamsArrayPtr)[
HC] =
Hc;
(*defaultParamsArrayPtr)[
NT] =
nt;
(*defaultParamsArrayPtr)[
NC] =
nc;
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"LAMBDA: " << (*defaultParamsArrayPtr)[
LAMBDA];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"MU: " << (*defaultParamsArrayPtr)[
MU];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"NUP: " << (*defaultParamsArrayPtr)[
NUP];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"SIGMA_YT: " << (*defaultParamsArrayPtr)[
SIGMA_YT];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"SIGMA_YC: " << (*defaultParamsArrayPtr)[
SIGMA_YC];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"HT: " << (*defaultParamsArrayPtr)[
HT];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"HC: " << (*defaultParamsArrayPtr)[
HC];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"NT: " << (*defaultParamsArrayPtr)[
NT];
MOFEM_LOG(
"ADOLCPlasticityWold", Sev::inform)
<<
"NC: " << (*defaultParamsArrayPtr)[
NC];
};
boost::ptr_deque<ForcesAndSourcesCore::UserDataOperator> &pip,
std::string block_name,
Sev sev) {
return 0;
}
recalculate_elastic_tangent = true;
return 0;
}
auto t_voight_total_strain = getFTensor1FromPtr<6>(&
a_sTrain[0]);
t_voight_strain_op(
i,
j,
Z) * t_voight_plastic_strain(
Z);
}
auto t_vioght_stress = getFTensor1FromPtr<6>(&
a_sTress[0]);
tStress(
i,
j) = t_voight_stress_op(
i,
j,
Z) * t_vioght_stress(
Z);
}
}
double alpha =
}
};
template <typename MODEL>
std::array<int, ClosestPointProjection::LAST_TAPE> tapes_tags = {0, 1, 2}) {
auto cp_ptr = boost::make_shared<MODEL>();
cp_ptr->getDefaultMaterialParameters();
cp_ptr->createMatAVecR();
cp_ptr->snesCreate();
cp_ptr->recordTapes();
cp_ptr->tapesTags = tapes_tags;
return cp_ptr;
}
}
#endif //__ADOLC_MATERIAL_MODELS_HPP





(follow the link on the badge).
